research paper about statistics and probability

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Indian J Anaesth
• v.60(9); 2016 Sep

Basic statistical tools in research and data analysis

Zulfiqar ali.

Department of Anaesthesiology, Division of Neuroanaesthesiology, Sheri Kashmir Institute of Medical Sciences, Soura, Srinagar, Jammu and Kashmir, India

S Bala Bhaskar

1 Department of Anaesthesiology and Critical Care, Vijayanagar Institute of Medical Sciences, Bellary, Karnataka, India

Statistical methods involved in carrying out a study include planning, designing, collecting data, analysing, drawing meaningful interpretation and reporting of the research findings. The statistical analysis gives meaning to the meaningless numbers, thereby breathing life into a lifeless data. The results and inferences are precise only if proper statistical tests are used. This article will try to acquaint the reader with the basic research tools that are utilised while conducting various studies. The article covers a brief outline of the variables, an understanding of quantitative and qualitative variables and the measures of central tendency. An idea of the sample size estimation, power analysis and the statistical errors is given. Finally, there is a summary of parametric and non-parametric tests used for data analysis.

INTRODUCTION

Statistics is a branch of science that deals with the collection, organisation, analysis of data and drawing of inferences from the samples to the whole population.[ 1 ] This requires a proper design of the study, an appropriate selection of the study sample and choice of a suitable statistical test. An adequate knowledge of statistics is necessary for proper designing of an epidemiological study or a clinical trial. Improper statistical methods may result in erroneous conclusions which may lead to unethical practice.[ 2 ]

Variable is a characteristic that varies from one individual member of population to another individual.[ 3 ] Variables such as height and weight are measured by some type of scale, convey quantitative information and are called as quantitative variables. Sex and eye colour give qualitative information and are called as qualitative variables[ 3 ] [ Figure 1 ].

Classification of variables

Quantitative variables

Quantitative or numerical data are subdivided into discrete and continuous measurements. Discrete numerical data are recorded as a whole number such as 0, 1, 2, 3,… (integer), whereas continuous data can assume any value. Observations that can be counted constitute the discrete data and observations that can be measured constitute the continuous data. Examples of discrete data are number of episodes of respiratory arrests or the number of re-intubations in an intensive care unit. Similarly, examples of continuous data are the serial serum glucose levels, partial pressure of oxygen in arterial blood and the oesophageal temperature.

A hierarchical scale of increasing precision can be used for observing and recording the data which is based on categorical, ordinal, interval and ratio scales [ Figure 1 ].

Categorical or nominal variables are unordered. The data are merely classified into categories and cannot be arranged in any particular order. If only two categories exist (as in gender male and female), it is called as a dichotomous (or binary) data. The various causes of re-intubation in an intensive care unit due to upper airway obstruction, impaired clearance of secretions, hypoxemia, hypercapnia, pulmonary oedema and neurological impairment are examples of categorical variables.

Ordinal variables have a clear ordering between the variables. However, the ordered data may not have equal intervals. Examples are the American Society of Anesthesiologists status or Richmond agitation-sedation scale.

Interval variables are similar to an ordinal variable, except that the intervals between the values of the interval variable are equally spaced. A good example of an interval scale is the Fahrenheit degree scale used to measure temperature. With the Fahrenheit scale, the difference between 70° and 75° is equal to the difference between 80° and 85°: The units of measurement are equal throughout the full range of the scale.

Ratio scales are similar to interval scales, in that equal differences between scale values have equal quantitative meaning. However, ratio scales also have a true zero point, which gives them an additional property. For example, the system of centimetres is an example of a ratio scale. There is a true zero point and the value of 0 cm means a complete absence of length. The thyromental distance of 6 cm in an adult may be twice that of a child in whom it may be 3 cm.

STATISTICS: DESCRIPTIVE AND INFERENTIAL STATISTICS

Descriptive statistics[ 4 ] try to describe the relationship between variables in a sample or population. Descriptive statistics provide a summary of data in the form of mean, median and mode. Inferential statistics[ 4 ] use a random sample of data taken from a population to describe and make inferences about the whole population. It is valuable when it is not possible to examine each member of an entire population. The examples if descriptive and inferential statistics are illustrated in Table 1 .

Example of descriptive and inferential statistics

Descriptive statistics

The extent to which the observations cluster around a central location is described by the central tendency and the spread towards the extremes is described by the degree of dispersion.

Measures of central tendency

The measures of central tendency are mean, median and mode.[ 6 ] Mean (or the arithmetic average) is the sum of all the scores divided by the number of scores. Mean may be influenced profoundly by the extreme variables. For example, the average stay of organophosphorus poisoning patients in ICU may be influenced by a single patient who stays in ICU for around 5 months because of septicaemia. The extreme values are called outliers. The formula for the mean is

where x = each observation and n = number of observations. Median[ 6 ] is defined as the middle of a distribution in a ranked data (with half of the variables in the sample above and half below the median value) while mode is the most frequently occurring variable in a distribution. Range defines the spread, or variability, of a sample.[ 7 ] It is described by the minimum and maximum values of the variables. If we rank the data and after ranking, group the observations into percentiles, we can get better information of the pattern of spread of the variables. In percentiles, we rank the observations into 100 equal parts. We can then describe 25%, 50%, 75% or any other percentile amount. The median is the 50 th percentile. The interquartile range will be the observations in the middle 50% of the observations about the median (25 th -75 th percentile). Variance[ 7 ] is a measure of how spread out is the distribution. It gives an indication of how close an individual observation clusters about the mean value. The variance of a population is defined by the following formula:

where σ 2 is the population variance, X is the population mean, X i is the i th element from the population and N is the number of elements in the population. The variance of a sample is defined by slightly different formula:

where s 2 is the sample variance, x is the sample mean, x i is the i th element from the sample and n is the number of elements in the sample. The formula for the variance of a population has the value ‘ n ’ as the denominator. The expression ‘ n −1’ is known as the degrees of freedom and is one less than the number of parameters. Each observation is free to vary, except the last one which must be a defined value. The variance is measured in squared units. To make the interpretation of the data simple and to retain the basic unit of observation, the square root of variance is used. The square root of the variance is the standard deviation (SD).[ 8 ] The SD of a population is defined by the following formula:

where σ is the population SD, X is the population mean, X i is the i th element from the population and N is the number of elements in the population. The SD of a sample is defined by slightly different formula:

where s is the sample SD, x is the sample mean, x i is the i th element from the sample and n is the number of elements in the sample. An example for calculation of variation and SD is illustrated in Table 2 .

Example of mean, variance, standard deviation

Normal distribution or Gaussian distribution

Most of the biological variables usually cluster around a central value, with symmetrical positive and negative deviations about this point.[ 1 ] The standard normal distribution curve is a symmetrical bell-shaped. In a normal distribution curve, about 68% of the scores are within 1 SD of the mean. Around 95% of the scores are within 2 SDs of the mean and 99% within 3 SDs of the mean [ Figure 2 ].

Normal distribution curve

Skewed distribution

It is a distribution with an asymmetry of the variables about its mean. In a negatively skewed distribution [ Figure 3 ], the mass of the distribution is concentrated on the right of Figure 1 . In a positively skewed distribution [ Figure 3 ], the mass of the distribution is concentrated on the left of the figure leading to a longer right tail.

Curves showing negatively skewed and positively skewed distribution

Inferential statistics

In inferential statistics, data are analysed from a sample to make inferences in the larger collection of the population. The purpose is to answer or test the hypotheses. A hypothesis (plural hypotheses) is a proposed explanation for a phenomenon. Hypothesis tests are thus procedures for making rational decisions about the reality of observed effects.

Probability is the measure of the likelihood that an event will occur. Probability is quantified as a number between 0 and 1 (where 0 indicates impossibility and 1 indicates certainty).

In inferential statistics, the term ‘null hypothesis’ ( H 0 ‘ H-naught ,’ ‘ H-null ’) denotes that there is no relationship (difference) between the population variables in question.[ 9 ]

Alternative hypothesis ( H 1 and H a ) denotes that a statement between the variables is expected to be true.[ 9 ]

The P value (or the calculated probability) is the probability of the event occurring by chance if the null hypothesis is true. The P value is a numerical between 0 and 1 and is interpreted by researchers in deciding whether to reject or retain the null hypothesis [ Table 3 ].

P values with interpretation

If P value is less than the arbitrarily chosen value (known as α or the significance level), the null hypothesis (H0) is rejected [ Table 4 ]. However, if null hypotheses (H0) is incorrectly rejected, this is known as a Type I error.[ 11 ] Further details regarding alpha error, beta error and sample size calculation and factors influencing them are dealt with in another section of this issue by Das S et al .[ 12 ]

Illustration for null hypothesis

PARAMETRIC AND NON-PARAMETRIC TESTS

Numerical data (quantitative variables) that are normally distributed are analysed with parametric tests.[ 13 ]

Two most basic prerequisites for parametric statistical analysis are:

• The assumption of normality which specifies that the means of the sample group are normally distributed
• The assumption of equal variance which specifies that the variances of the samples and of their corresponding population are equal.

However, if the distribution of the sample is skewed towards one side or the distribution is unknown due to the small sample size, non-parametric[ 14 ] statistical techniques are used. Non-parametric tests are used to analyse ordinal and categorical data.

Parametric tests

The parametric tests assume that the data are on a quantitative (numerical) scale, with a normal distribution of the underlying population. The samples have the same variance (homogeneity of variances). The samples are randomly drawn from the population, and the observations within a group are independent of each other. The commonly used parametric tests are the Student's t -test, analysis of variance (ANOVA) and repeated measures ANOVA.

Student's t -test

Student's t -test is used to test the null hypothesis that there is no difference between the means of the two groups. It is used in three circumstances:

where X = sample mean, u = population mean and SE = standard error of mean

where X 1 − X 2 is the difference between the means of the two groups and SE denotes the standard error of the difference.

• To test if the population means estimated by two dependent samples differ significantly (the paired t -test). A usual setting for paired t -test is when measurements are made on the same subjects before and after a treatment.

The formula for paired t -test is:

where d is the mean difference and SE denotes the standard error of this difference.

The group variances can be compared using the F -test. The F -test is the ratio of variances (var l/var 2). If F differs significantly from 1.0, then it is concluded that the group variances differ significantly.

Analysis of variance

The Student's t -test cannot be used for comparison of three or more groups. The purpose of ANOVA is to test if there is any significant difference between the means of two or more groups.

In ANOVA, we study two variances – (a) between-group variability and (b) within-group variability. The within-group variability (error variance) is the variation that cannot be accounted for in the study design. It is based on random differences present in our samples.

However, the between-group (or effect variance) is the result of our treatment. These two estimates of variances are compared using the F-test.

A simplified formula for the F statistic is:

where MS b is the mean squares between the groups and MS w is the mean squares within groups.

Repeated measures analysis of variance

As with ANOVA, repeated measures ANOVA analyses the equality of means of three or more groups. However, a repeated measure ANOVA is used when all variables of a sample are measured under different conditions or at different points in time.

As the variables are measured from a sample at different points of time, the measurement of the dependent variable is repeated. Using a standard ANOVA in this case is not appropriate because it fails to model the correlation between the repeated measures: The data violate the ANOVA assumption of independence. Hence, in the measurement of repeated dependent variables, repeated measures ANOVA should be used.

Non-parametric tests

When the assumptions of normality are not met, and the sample means are not normally, distributed parametric tests can lead to erroneous results. Non-parametric tests (distribution-free test) are used in such situation as they do not require the normality assumption.[ 15 ] Non-parametric tests may fail to detect a significant difference when compared with a parametric test. That is, they usually have less power.

As is done for the parametric tests, the test statistic is compared with known values for the sampling distribution of that statistic and the null hypothesis is accepted or rejected. The types of non-parametric analysis techniques and the corresponding parametric analysis techniques are delineated in Table 5 .

Analogue of parametric and non-parametric tests

Median test for one sample: The sign test and Wilcoxon's signed rank test

The sign test and Wilcoxon's signed rank test are used for median tests of one sample. These tests examine whether one instance of sample data is greater or smaller than the median reference value.

This test examines the hypothesis about the median θ0 of a population. It tests the null hypothesis H0 = θ0. When the observed value (Xi) is greater than the reference value (θ0), it is marked as+. If the observed value is smaller than the reference value, it is marked as − sign. If the observed value is equal to the reference value (θ0), it is eliminated from the sample.

If the null hypothesis is true, there will be an equal number of + signs and − signs.

The sign test ignores the actual values of the data and only uses + or − signs. Therefore, it is useful when it is difficult to measure the values.

Wilcoxon's signed rank test

There is a major limitation of sign test as we lose the quantitative information of the given data and merely use the + or – signs. Wilcoxon's signed rank test not only examines the observed values in comparison with θ0 but also takes into consideration the relative sizes, adding more statistical power to the test. As in the sign test, if there is an observed value that is equal to the reference value θ0, this observed value is eliminated from the sample.

Wilcoxon's rank sum test ranks all data points in order, calculates the rank sum of each sample and compares the difference in the rank sums.

Mann-Whitney test

It is used to test the null hypothesis that two samples have the same median or, alternatively, whether observations in one sample tend to be larger than observations in the other.

Mann–Whitney test compares all data (xi) belonging to the X group and all data (yi) belonging to the Y group and calculates the probability of xi being greater than yi: P (xi > yi). The null hypothesis states that P (xi > yi) = P (xi < yi) =1/2 while the alternative hypothesis states that P (xi > yi) ≠1/2.

Kolmogorov-Smirnov test

The two-sample Kolmogorov-Smirnov (KS) test was designed as a generic method to test whether two random samples are drawn from the same distribution. The null hypothesis of the KS test is that both distributions are identical. The statistic of the KS test is a distance between the two empirical distributions, computed as the maximum absolute difference between their cumulative curves.

Kruskal-Wallis test

The Kruskal–Wallis test is a non-parametric test to analyse the variance.[ 14 ] It analyses if there is any difference in the median values of three or more independent samples. The data values are ranked in an increasing order, and the rank sums calculated followed by calculation of the test statistic.

Jonckheere test

In contrast to Kruskal–Wallis test, in Jonckheere test, there is an a priori ordering that gives it a more statistical power than the Kruskal–Wallis test.[ 14 ]

Friedman test

The Friedman test is a non-parametric test for testing the difference between several related samples. The Friedman test is an alternative for repeated measures ANOVAs which is used when the same parameter has been measured under different conditions on the same subjects.[ 13 ]

Tests to analyse the categorical data

Chi-square test, Fischer's exact test and McNemar's test are used to analyse the categorical or nominal variables. The Chi-square test compares the frequencies and tests whether the observed data differ significantly from that of the expected data if there were no differences between groups (i.e., the null hypothesis). It is calculated by the sum of the squared difference between observed ( O ) and the expected ( E ) data (or the deviation, d ) divided by the expected data by the following formula:

A Yates correction factor is used when the sample size is small. Fischer's exact test is used to determine if there are non-random associations between two categorical variables. It does not assume random sampling, and instead of referring a calculated statistic to a sampling distribution, it calculates an exact probability. McNemar's test is used for paired nominal data. It is applied to 2 × 2 table with paired-dependent samples. It is used to determine whether the row and column frequencies are equal (that is, whether there is ‘marginal homogeneity’). The null hypothesis is that the paired proportions are equal. The Mantel-Haenszel Chi-square test is a multivariate test as it analyses multiple grouping variables. It stratifies according to the nominated confounding variables and identifies any that affects the primary outcome variable. If the outcome variable is dichotomous, then logistic regression is used.

SOFTWARES AVAILABLE FOR STATISTICS, SAMPLE SIZE CALCULATION AND POWER ANALYSIS

Numerous statistical software systems are available currently. The commonly used software systems are Statistical Package for the Social Sciences (SPSS – manufactured by IBM corporation), Statistical Analysis System ((SAS – developed by SAS Institute North Carolina, United States of America), R (designed by Ross Ihaka and Robert Gentleman from R core team), Minitab (developed by Minitab Inc), Stata (developed by StataCorp) and the MS Excel (developed by Microsoft).

There are a number of web resources which are related to statistical power analyses. A few are:

• StatPages.net – provides links to a number of online power calculators
• G-Power – provides a downloadable power analysis program that runs under DOS
• Power analysis for ANOVA designs an interactive site that calculates power or sample size needed to attain a given power for one effect in a factorial ANOVA design
• SPSS makes a program called SamplePower. It gives an output of a complete report on the computer screen which can be cut and paste into another document.

It is important that a researcher knows the concepts of the basic statistical methods used for conduct of a research study. This will help to conduct an appropriately well-designed study leading to valid and reliable results. Inappropriate use of statistical techniques may lead to faulty conclusions, inducing errors and undermining the significance of the article. Bad statistics may lead to bad research, and bad research may lead to unethical practice. Hence, an adequate knowledge of statistics and the appropriate use of statistical tests are important. An appropriate knowledge about the basic statistical methods will go a long way in improving the research designs and producing quality medical research which can be utilised for formulating the evidence-based guidelines.

Financial support and sponsorship

Conflicts of interest.

There are no conflicts of interest.

Research on Teaching and Learning Probability

• Open Access
• First Online: 13 July 2016

Cite this chapter

You have full access to this open access chapter

• Carmen Batanero 7 ,
• Egan J. Chernoff 8 ,
• Joachim Engel 9 ,
• Hollylynne S. Lee 10 &
• Ernesto Sánchez 11  

Part of the book series: ICME-13 Topical Surveys ((ICME13TS))

33k Accesses

20 Citations

Research in probability education is now well established and tries to improve the challenges posed in the education of students and teachers. In this survey on the state of the art, we summarise existing research in probability education before pointing to some ideas and questions that may help in framing a future research agenda.

• Mathematics Education
• Prospective Teacher
• Probabilistic Reasoning
• School Curriculum
• Sample Space

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

C. Batanero, E. Chernoff, J. Engel, H. Lee, and E. Sánchez

You have full access to this open access chapter,  Download chapter PDF

1 Introduction

To adequately function in society, citizens need to overcome their deterministic thinking and accept the existence of fundamental chance in nature. At the same time, they need to acquire strategies and ways of reasoning that help them in making adequate decisions in everyday and professional situations where chance is present.

This need for probability literacy has been recognized by educational authorities in many countries by including probability in the curricula at different educational levels and in the education of teachers. However, including a topic in the curriculum does not automatically assure its correct teaching and learning; the specific characteristics of probability, such as a multifaceted view of probability or the lack of reversibility of random experiments, are not usually found in other areas and will create special challenges for teachers and students.

Research in probability education tries to respond to the above challenges and it is now well established, as shown by the Teaching and Learning of Probability Topic Study Group at the 13th International Congress of Mathematics Education (ICME). Probability education research is also visible in the many papers on this topic presented at conferences such as the European Mathematics Education Conference (CERME), the International Conference on Teaching Statistics (ICOTS), as well as in regional or national conferences such as the Latin-America Mathematics Education Conference (RELME).

Furthermore, several books and major handbook chapters listed in the Further Readings section suggest the relevance of this field and the need to (re)formulate a research agenda in this area for the coming years. In this survey on the state of the art, we summarise existing research in probability education before pointing to some ideas and questions that may help in framing a future research agenda.

2 Survey on the State of the Art

Research in probability education has a fairly long history and includes theoretical analyses and empirical research on a variety of topics and from different perspectives, as described in the next sections. As we reviewed the existing literature on probability education, several major themes came to the fore. These themes have been used to organize a brief review of our current understanding of probability education that informs the discussions for the 2016 ICME topic study group.

2.1 The Nature of Chance and Probability

Research in any area of mathematics education should be supported by an epistemological reflection about the objects that are being investigated. This reflection is especially relevant when focusing on probability, where different approaches to the concept that influence both the practice of stochastics and the school curricula are still being debated in the scientific community.

According to Hacking ( 1975 ), probability was conceived from two main, albeit different, perspectives since its emergence. A statistical side of probability is related to the need to find the objective mathematical rules that govern random processes; probability values are assigned through data collected from surveys and experiments. Complementary to this vision, an epistemic side views probability as a personal degree of belief, which depends on information available to the person assigning a probability. From these two main perspectives, which are reflected in the works of the main authors who have contributed to the progress of probability, different views of probability have been sustained through history (Batanero 2015 ; Batanero and Díaz 2007 ; Batanero et al. 2005a , b ; Borovcnik and Kapadia 2014a ; Chernoff and Russell 2012 ). Currently, the main primary interpretations are intuitive, classical, frequentist, subjective, logical, propensity, and axiomatic. Each of these views entails some philosophical issues and is more suited to model particular real-world phenomena or to be taken into account in curricula for specific students.

In the next sections we briefly summarise the main features of the aforementioned views of probabilities, part of which have been introduced in school curricula.

2.1.1 Intuitive View of Probability

The theory of probability is, in essence, a formal encapsulation of intuitive views of chance that lead to the fundamental idea of assigning numbers to uncertain events. Intuitive ideas about chance emerged very early in history in many different cultures and were linked to problems related to setting fair betting in games of chance (Batanero and Díaz 2007 ; Bennet 1999 ). According to David ( 1962 ), cubic dice were abundant in primitive cultures (e.g., the Egyptian, Chinese, Greek and Roman civilizations), which used games of chance in an attempt to predict or control fate in decision-making or religious ceremonies. Interestingly, the development of the theory of probability is much more recent with, according to David ( 1962 ), no clear reasons to explain this delay.

Intuitive ideas about chance and probability also appear in young children who use qualitative expressions (such as terms “probable” or “unlikely”) to express their degrees of belief in the occurrence of random events. These intuitive ideas can be used by a teacher to help children develop a more mature understanding and use probability as a tool to compare likelihood of different events in a world filled with uncertainty.

2.1.2 Classical Meaning

The earlier theoretical progress in probability theory was linked to games of chance such as throwing dice. For example, in his correspondence with Fermat, Pascal (1654/ 1963 ) solved the problem of estimating the fair amount to be given to each player if the game is interrupted by “force majeure” by proportionally dividing the stakes among each player’s chances. In another example, Cardano (1663/ 1961 ) advised players to consider the number of total possibilities and the number of ways favourable results can occur and to compare the two numbers in order to make a fair bet.

It is not surprising that the initial formalization of this concept was based on an assumption that all possible elementary events were equiprobable, since this hypothesis is reasonable in many chance games. In the classical definition of probability, given by Abraham de Moivre in 1718 in Doctrine of Chances and later refined by Laplace in 1814 in his Philosophical Essay on Probability , probability is simply a fraction of the number of favourable cases to a particular event divided by the number of all cases possible. This definition has been widely criticised since its publication, since the assumption of equiprobability of outcomes is subjective and it impedes the application of probability to a broad variety of natural phenomena where this assumption may not be valid.

2.1.3 Frequentist Meaning

The convergence of relative frequencies for the same event to a constant value after a large number of independent identical trials of a random experiment has been observed by many authors. In trying to extend the scope of probability to life-expectancy and insurance problems, Bernoulli (1713/ 1987 ) proved a first version of the Law of Large Numbers . According to this theorem, the relative frequency \( h_{n} \) for a given event in a large number of trials should be close to the theoretical probability p of that event and tend to become closer as more trials are performed. Footnote 1 Given that stabilised frequencies are observable, this theorem was also considered as a proof of the objective character of probability (Fine 1971 ).

In this frequentist approach, sustained later by von Mises (1928/ 1952 ) and Renyi (1966/ 1992 ), probability is defined as the hypothetical number towards which the relative frequency tends when a random experiment is repeated infinitely many times.

Since such an empirical tendency is visible in many natural phenomena, this particular definition of probability extended the range of applications enormously.

A practical drawback of this frequentist view is that we only obtain an estimation of probability that varies from one series of repetitions of experiments (called samples) to another. Moreover, this approach is not appropriate when it is not possible to repeat an experiment under exactly the same conditions (Batanero et al. 2005a , b ). Consequently, it is important to make clear to students the difference between a theoretical model of probability and the frequency data from reality used to create a model of probability. Sometimes this difference is not made explicit in the classroom and may confuse students who need to use abstract knowledge about probability to solve concrete problems from real life.

2.1.4 Propensity Meaning

Popper ( 1959 ) introduced the idea of propensity as a measure of the tendency of a random system to behave in a certain way and as a physical disposition to produce an outcome of a certain kind. In the same sense, Peirce (1910/ 1932 ) proposed a concept of probability according to which a die, for example, possesses expected dispositions for its various possible outcomes; these propensities are directly related to the long-run trends and indirectly to singular events.

In the long run, propensities are tendencies to produce relative frequencies with particular values, but the propensities are not the probability values themselves (Gillies 2000 ). For example, a cube-shaped die has an extremely strong tendency (i.e., propensity) to produce a 5 when rolled with long-run relative frequency of 1/6. The probability value 1/6 is small, so it does not measure this strong tendency. In single-case theory (e.g., Mellor 1971 ) the propensities are identical to the probability values and are considered as probabilistic causal tendencies to produce a particular result on a specific occasion.

Again this propensity interpretation of probability is controversial. In the long-run interpretation, propensity is not expressed in terms of other empirically verifiable quantities, and we then have no method of empirically finding the value of a propensity. With regards to the single-case interpretation, it is difficult to assign an objective probability for single events (Gillies 2000 ). It is also unclear whether single-case propensity theories obey the probability calculus or not.

2.1.5 Logical Meaning

Researchers such as Keynes ( 1921 ) and Carnap ( 1950 ) developed the logical theories of probability, which retain the classical idea that probabilities can be determined a priori by an examination of the space of possibilities; however, the possibilities may be assigned unequal weights. In this view, probability is a degree of implication that measures the support provided by some evidence E to a given hypothesis H. Between certainty (1) and impossibility (0), all other degrees of probability are possible. This view amplifies deductive logic, since implication and incompatibility can be considered as extreme cases of probability.

Carnap ( 1950 ) constructed a formal language and defined probability as a rational degree of confirmation. The degree of confirmation of one hypothesis H, given some evidence E , is a conditional probability and depends entirely on the logical and semantic properties of H and E and the relations between them. Therefore, probability is only defined for the particular formal language in which these relations are made explicit.

Another problem in this approach is that there are many possible confirmation functions, depending on the possible choices of initial measures and on the language in which the hypothesis is stated. A further problem is selecting the adequate evidence E in an objective way, since the amount of evidence might vary from one person to another (Batanero and Díaz 2007 ).

2.1.6 Subjective Meaning

In the previous approaches presented, probability is an “objective” value that we assign to each event. However, Bayes’ theorem, published in 1763, proved that the probability for an event can be revised in light of new available data. A simple version this theorem establishes that, when the “prior” probabilities \( P(A_{i} ) \) and the likelihood \( P(B|A_{i} ) \) to obtain B for each \( A_{i} \) are known for a number of incompatible events \( A_{i} \) such that \( \mathop {\bigcup }\nolimits_{1 = 1}^{n} {A_i}= E \) , then it holds:

Using Bayes’ theorem, an initial (prior) probability can be transformed into a posterior probability using new data and probability loses its objective character. Following this interpretation, some mathematicians (e.g., Keynes, Ramsey and de Finetti) considered probability as a personal degree of belief that depends on a person’s knowledge or experience. However, the status of the prior distribution in this approach was criticised as subjective, even if the impact of the prior diminishes by objective data, and de Finetti proposed a system of axioms to justify this view in 1937.

In this subjectivist viewpoint, the repetition of the same situation is no longer necessary to give a sense to probability, and for this reason the applications of probability entered new fields such as politics and economy, where it is difficult to assure replications of experiments. Today the Bayesian approach to inference, which is based in this approach, is quickly gaining further traction in numerous fields.

2.1.7 Axiomatic Theory

Despite the strong philosophical discussion on the foundations, the applications of probability to all sciences and sectors of human activity expanded very quickly. Throughout the 20th century, different mathematicians tried to formalise the mathematical theory of probability. Following Borel’s work on set and measure theory, Kolmogorov (1933/ 1950 ), who corroborated the frequentist view, derived an axiomatic theory.

The set S of all possible outcomes of a random experiment is called the sample space of the experiment. Footnote 2 In order to define probability a set algebra A containing subsets of the sample space and which is closed under numerable union and complement operations is considered. Footnote 3 The complement of an event \( \bar{A} \) is made of all the outcomes that do not take part in A . The event \( S = A\mathop \cup \nolimits \bar{A} \) always happens and is called a certain event.

Probability is any function defined from A in the interval of real numbers [0,1] that fulfils the following three axioms, from which many probability properties and theorems can be deduced:

\( 0 \le P\left( A \right) \le 1 \) , for every \( A \in \varvec{A} \) ;

\( P\left( S \right) = 1 \) ;

(a) For a finite sample space S and incompatible or disjoint events A and B , i.e., \( A\mathop \cap \nolimits B = \emptyset \) , it holds that \( P\left( {A\mathop \cup \nolimits B} \right) = P\left( A \right) + P\left( B \right). \)

(b) For an infinite sample space S and a countable collection of pairwise disjoint sets \( A _{i} , i = 1,2, \ldots \) it holds, \( P\left( {\bigcup\nolimits_{i = 1}^{\infty } {A_{i } } } \right) = \sum\nolimits_{i = 1}^{\infty } {P(A_{i} )} . \)

This axiomatic theory was accepted by the different probability schools because, with some compromise, the mathematics of probability (classical, frequentist or subjective) may be encoded by Kolmogorov’s theory. However, the interpretation of what is a probability would differ according to the perspective one adheres to; the discussion about the meanings of probability is still very much alive in different approaches to statistics. This link between probability and philosophy may also explain people’s intuitions that often conflict with the mathematical rules of probability (Borovcnik et al. 1991 ).

2.1.8 Summary of Different Views

Our exposition suggests that the different views of probability described involve specific differences, not only in the definition of probability itself, but also in the related concepts, properties, and procedures that have emerged to solve various problems related to each view. We summarise some of these differences in Table  1 , partially adapted from Batanero and Díaz ( 2007 ).

2.1.9 Different Views of Probability in School Curricula

The above debates were, and are, reflected in school curricula, although not all the approaches to probability received the same interest. Before 1970, the classical view of probability based on combinatorial calculus dominated the secondary school curriculum in countries such as France (Henry 2010 ). Since this view relies strongly on combinatorial reasoning, the study of probability, beyond very simple problems, was difficult for students.

The axiomatic approach was also dominant in the modern mathematics era because probability was used as a relevant example of the power of set theory. However, in both the classical and axiomatic approaches, multiple applications of probability to different sciences were hidden to students. Consequently, probability was considered by many secondary school teachers as a subsidiary part of mathematics, dealing only with chance games, and there was a tendency to “reduce” the teaching of probability (Batanero 2015 ).

Today, with the increasing interest in statistics and technology developments, the frequentist approach is receiving preferential treatment. An experimental introduction of probability as a limit of relative frequencies is suggested in many curricula and standards documents (e.g., the Common Core State Standards in Mathematics [CCSSI] 2010 ; the Ministerio de Educación, Cultura y Deporte [MECD] 2014 ; and the National Council of Teachers of Mathematics [NCTM] 2000 ), and probability is presented as a theoretical tool used to approach problems that arise from statistical experiences. At the primary school level, an intuitive view, where children start from their intuitive ideas related to chance and probability, is also favoured. The axiomatic approach is not used at the school level, being too formal and adequate only for those who follow studies of pure mathematics at the post-secondary level. More details of probability contents in the school curricula will be discussed in Sect.  2.3 .

2.2 Probabilistic Knowledge and Reasoning

The recent emphasis on the frequentist view and on informal approaches in the teaching of inference may lead to a temptation to reduce teaching probability to the teaching of simulations—with little reflection on probability rules. However, as described by Gal ( 2005 ), probability knowledge and reasoning is needed in everyday and professional settings for all citizens in decision-making situations (e.g., stock market, medical diagnosis, voting, and many others), as well as to understand sampling and inference, even in informal approaches. Moreover, when considering the training of scientists or professionals (e.g., engineers, doctors) at university level, a more complex knowledge of probability is required. Consequently, designing educational programmes that help develop probability knowledge and reasoning for a variety of students requires the description of its different components.

While there is an intense discussion on the nature of statistical thinking and how it differs from statistical reasoning and statistical literacy (e.g., Ben-Zvi and Garfield 2004 ), the discussion of core components of probabilistic reasoning is still a research concern. Below we describe some points to advance future research on this topic.

2.2.1 What Is Probabilistic Reasoning?

Probability constitutes a distinct approach to thinking and reasoning about real-life phenomena. Probabilistic reasoning is a mode of reasoning that refers to judgments and decision-making under uncertainty and is relevant to real life, for example, when evaluating risks (Falk and Konold 1992 ). It is thinking in scenarios that allow for the exploration and evaluation of different possible outcomes in situations of uncertainty. Thus, probabilistic reasoning includes the ability to:

Identify random events in nature, technology, and society;

Analyse conditions of such events and derive appropriate modelling assumptions;

Construct mathematical models for stochastic situations and explore various scenarios and outcomes from these models; and

Apply mathematical methods and procedures of probability and statistics.

An important step in any application of probability to real-world phenomena is modelling random situations (Chaput et al. 2011 ). Probability models, such as the binomial or normal distribution, supply us with the means to structure reality: they constitute important tools to recognise and to solve problems. Probability-related knowledge relevant to understanding real-life situations includes concepts such as conditional probabilities, proportional reasoning, random variables, and expectation. It is also important to be able to critically assess the application of probabilistic models of real phenomena. Since today an increasing number of events are described in terms of risk, the underlying concepts and reasoning have to be learned in school, and the understanding of risk by children should also be investigated (Martignon 2014 ; Pange and Talbot 2003 ).

2.2.2 Paradoxes and Counterintuitive Results

Probabilistic reasoning is different from reasoning in classical two-valued logic, where a statement is either true or false. Probabilistic reasoning follows different rules than classical logic. A famous example, where the transitivity of preferences does not hold, is Efron’s intransitive dice (Savage 1994 ), where the second person who selects a die to play always has an advantage in the game (no matter which die their opponent first chooses).

Furthermore, the field of probability is replete with intuitive challenges and paradoxes, while misconceptions and fallacies are abundant (Borovcnik and Kapadia 2014b ). These counterintuitive results also appear in elementary probability, while in other areas of mathematics counterintuitive results only happen when working with advanced concepts (Batanero 2013 ; Borovcnik 2011 ). For example, it is counterintuitive that obtaining a run of four consecutive heads when tossing a fair coin does not affect the probability that the following coin flip will result in heads (i.e., the gambler’s fallacy).

Probability utilises language and terminology that is demanding and is not always identical to the notation common in other areas of mathematics (e.g., the use of Greek or capital letters to denote random variables). Yet, probability provides an important thinking mode on its own, not just a precursor of inferential statistics. The important contribution of probability to solve real problems justifies its inclusion into school curriculum.

2.2.3 Causality and Conditioning

Another component of probabilistic reasoning is distinguishing between causality and conditioning. Although independence is mathematically reduced to the multiplicative rule, a didactical analysis of independence should include discussion of the relationships between stochastic and physical independence and of psychological issues related to causal explanation that people often relate to independence (Borovcnik 2012 ). While dependence in probability characterises a bi-directional relation, the two directions involved in conditional probabilities have a completely different connotation from a causal standpoint. For example, whereas the conditional probability of having some virus to having a positive result on a diagnostic test is causal, the backward direction of conditional probability from a positive diagnosis to actually having the virus is merely indicative. Alternatively stated, while the test is positive because of a disease, no disease is caused by a positive test result.

In many real-life situations the causal and probabilistic approach are intermingled. Often we observe phenomena that have a particular behaviour due to some causal impact factors plus some random perturbations. Then the challenge, often attacked with statistical methods, is to separate the causal from the random influence. A sound grasp of conditional probabilities is needed to understand all these situations, as well as for a foundation for understanding inferential statistics.

2.2.4 Random and Causal Variation

Another key element in probabilistic reasoning is discriminating random from causal variation. Variability is a key feature of any statistical data, and understanding of variation is a core element of statistical reasoning (Wild and Pfannkuch 1999 ). However, whereas variation of different samples from the same population or process (e.g., height of different students) may be attributed to random effects, the differences between samples from different populations (e.g., heights of boys and girls) are sometimes explained causally. Besides, the larger the size of the individual variation, the smaller the amount of variation that can be attributed to systematic causes.

A helpful metaphor in this regard is to separate the signal (the true causal difference) from the noise (the individual random variation) (Konold and Pollatsek 2002 ). Said authors characterise data analysis as the search for signals (causal variations) in noisy processes (which include random variation). Borovcnik ( 2005 ) introduced the structural equation, which represents data as decomposed into a signal to be recovered and noise. Figure  1 displays five expressions of the signal-noise idea from different perspectives. The structural equation is a core idea of modelling statistical data and is a metaphor for our human response to deal with an overwhelming magnitude of relevant and irrelevant information contained in observed data. How to separate causal from random sources of variation is by no means unique. Probability hereby acquires more the character of a heuristic tool to analyse reality.

Different versions of the structural equation

Random and causal sources of variation are complementary to each other, as they are considered in probability models used in statistical decision processes. Consider, for example, the problem of deciding whether expected values of two random variables differ. Several realisations of each of the two single variables will not be identical and most likely the empirical means will not be equal. Based on a sample of realisations of each random variable, we perform an analysis that leads to the classical two-sample statistical test. Statistical inference based on probabilistic reasoning provides methods and criteria to decide, with a margin of error, when the observed differences are due to random or causal variation.

It may be surprising, and from an epistemological point of view is far from obvious, that patterns of variation in careful measurements or in data of many individuals can be described by the same type of mathematics that is used to characterise the results of random experiments. Indeed, it is here where data and chance (i.e., statistics as the science of analysing data and probability as the study of random phenomena) come together to build the powerful foundation of statistical inference.

However, the above is not obvious for some students, who may reveal a prevailing inclination to attribute even small variation in observed phenomena to deterministic causes. As is the case in the following quote from a 17-year-old student: “I accept the idea of randomness when I ask for the sum of two dice, but what is random about the weight loss of a person following a particular diet plan?” (Engel et al. 2008 ). A perspective of losing weight as a noisy process may solve the problem for the student: sticking to a particular diet plan may have an influence on body weight over time, described by a (deterministic) function which, however, is affected by individual, unforeseen, and unpredictable random influences.

Wild and Pfannkuch ( 1999 ) state that people have a strong natural tendency to search for specific causes. This tendency leads people to search for causes even when an individual’s data are quite within the bounds of expected random variation. Konold ( 1989 ) has accounted for this tendency in his outcome approach . This tendency is, in particular, visible in secondary school students, whose adherence to a mechanistic-deterministic view of the world is well documented and does not seem to fade with increasing years of schooling (Engel and Sedlmeier 2005 ).

2.2.5 Probabilistic Versus Statistical Reasoning

To conclude this section we remark that probabilistic reasoning is closely related to, and yet different from, statistical reasoning. Statistics can be portrayed as the science of learning from data (Moore 2010 ). At first glance it may be surprising to recognize that data (from Latin datum , the given) can be connected with randomness as the unforeseen. The outcome of a random experiment is uncertain. How is it possible to associate measurement readings collected in a concrete physical context with the rather metaphysical concept of randomness, which even cannot be defined in exact mathematical terms?

While probabilistic reasoning aims at structuring our thinking through models, statistical reasoning tries to make sense of observed data by searching for models that may explain the data. Probabilistic reasoning usually starts with models, investigates various scenarios and attempts to predict possible realizations of random variables based on these models. The initial points of statistical reasoning are data, and suitable models are fitted to these data as a means to gain insight into the data-producing process. These different approaches may be reconciled by paraphrasing Immanuel Kant’s famous statement, “Theory without data is empty, data without theory is blind.” Both statistical reasoning and probabilistic reasoning alone have their limitations and their merits. Their full power for advancing human knowledge comes to bear only in the synthesis acknowledging that they are two sides of the same coin.

2.3 Probability in School Curricula

The described need to understand random phenomena and to make adequate decisions when confronted with uncertainty has been recognised by many educational authorities. Consequently, the teaching of probability is included in curricula in many countries during primary or secondary education. An important area of research in probability education is the analysis of curricular guidelines and curricular materials, such as textbooks. Both topics are now commented on in turn.

2.3.1 Probability in Primary School

At the beginning of this century, the Standards of the National Council of Teachers of Mathematics (NCTM 2000 ) in the United States included the following recommendations related to understanding and applying basic concepts of probability for children in Grades 3–5:

Describe events as likely or unlikely and discuss the degree of likelihood using such words as certain, equally likely, and impossible;

Predict the probability of outcomes of simple experiments and test the predictions;

Understand that the measure of the likelihood of an event can be represented by a number from 0 to 1.

Their recommendations have been reproduced in other curricular guidelines for Primary school. For example, in Spain (Ministerio de Educación y Ciencia [MEC] 2006 ), the language of chance and the difference between “certain,” “impossible,” and “possible” were introduced in Grades 1–2; in Grades 3–4 the suggestion was that children were encouraged to perform simple experiments and evaluate their results; and in Grades 5–6, children were expected to compare the likelihood of different events and make estimates for the probability of simple situations.

Today, some curricula include probability from the first or second levels of primary education (e.g., Australian Curriculum, Assessment and Reporting Authority [ACARA] 2010 ; MECD 2014 , 2015 ; Ministerio de Educación Pública [MEP] 2012 ; Ministry of Education [ME] 2007 ), while in other curricular guidelines probability has been delayed to either Level 6 or to secondary education (e.g., CCSSI 2010 ; Secretaría de Educación Pública [SEP] 2011 ). In the case of Mexico, for example, probability was postponed to the middle school level on the argument that primary school teachers have many difficulties in understanding probability and therefore are not well prepared to teach the topic.

A possible explanation for the tendency to delay teaching probability is its diminished emphasis in some statistics education researchers’ suggestions that statistical inference be taught with an informal approach. This change does not take into account, however, the relevance of educating probabilistic reasoning in young children, which was emphasised by Fischbein ( 1975 ), or the multiple connections between probability and other areas of mathematics as stated in the Guidelines for Assessment and Instruction in Statistics Education (GAISE) for pre-K-12 levels (Franklin et al. 2007 , p. 8): “Probability is an important part of any mathematical education. It is a part of mathematics that enriches the subject as a whole by its interactions with other uses of mathematics.”

2.3.2 Probability at the Middle and High School Levels

There has been a long tradition of teaching probability in middle and high school curricula where the topics taught include compound experiments and conditional probability. For example, the NCTM ( 2000 ) stated that students in Grades 6–8 should:

Understand and use appropriate terminology to describe complementary and mutually exclusive events;

Use proportionality and a basic understanding of probability to make and test conjectures about the results of experiments and simulations;

Compute probabilities for simple compound events, using such methods as organised lists, tree diagrams, and area models.

In Grades 9–12 students should:

Understand the concepts of sample space and probability distribution and construct sample spaces and distributions in simple cases;

Use simulations to construct empirical probability distributions;

Compute and interpret the expected value of random variables in simple cases;

Understand the concepts of conditional probability and independent events;

Understand how to compute the probability of a compound event.

Similar content was included, even reinforced, in other curricular guidelines, such as ACARA ( 2010 ), Kultusministerkonferenz (KMK) ( 2004 , 2012 ), MEC ( 2007a , b ), MECD ( 2015 ), and SEP ( 2011 ). For example, in Spain and South Australia the high school curriculum (MEC 2007b ; MECD 2015 ; Senior Secondary Board of South Australia (SSBSA) 2002 ) for social science students includes the binomial and normal distributions and an introduction to inference (sampling distributions, hypothesis tests, and confidence intervals). In Mexico, there are different high school strands; in most of them a compulsory course in probability and statistics is included. In France, the main statistical content in the last year of high school ( terminale , 17-year-olds) is statistical inference, e.g., confidence intervals, intuitive introduction to hypothesis testing (Raoult 2013 ). In the last level of high school, CCSSI ( 2010 ) also recommends that U.S. students use sample data and simulation models to estimate a population mean or proportion and develop a margin of error and that they use data from randomised experiments to compare two treatments and decide if differences between parameters are significant.

2.3.3 Fundamental Probabilistic Ideas

A key point in teaching probability is to reflect on the main content that should be included at different educational levels. Heitele ( 1975 ) suggested a list of fundamental probabilistic concepts that played a key role in the history of probability and are the basis for the modern theory of probability. At the same time, people frequently hold incorrect intuitions about their meaning or application in absence of instruction. This list includes the ideas of random experiment and sample space, the addition and multiplication rule, independence and conditional probability, random variables and distribution, combinations and permutations, convergence, sampling, and simulation. Below we briefly comment on some of these ideas, which were analysed by Batanero et al. ( 2005a , b ):

Randomness. Though randomness is a foundational concept in probability (random variation, random process, or experiment), it is a “fuzzy” concept, not always defined in textbooks. Research shows the coexistence of different interpretations as well as misconceptions held by students and suggests the need to reinforce understanding of randomness in students (Batanero 2015 ).

Events and sample space. Some children only concentrate on a single event since their thinking is mainly deterministic (Langrall and Mooney 2005 ). It is then important that children understand the need to take into account all different possible outcomes in an experiment to compute its probability.

Combinatorial enumeration and counting . Combinatorics is used in listing all the events in a sample space or in counting (without listing) all its elements. Although in the frequentist approach we do not need combinatorics to estimate the value of probability, combinatorial reasoning is nevertheless needed in other situations, for example, to understand how events in a compound experiment are formed or to understand how different samples of the same size can be selected from a population. Combinatorial reasoning is difficult; however, it is possible to use tools such as tree diagrams to help students reinforce this particular type of reasoning.

Independence and conditional probability. The notion of independence is important to understand simulations and the empirical estimates of probability via frequency, since when repeating experiments we require independence of trials. Computing probabilities in compound experiments requires one to analyse whether the experiments are dependent or not. Finally, the idea of conditional probability is needed to understand many concepts in probability and statistics, such as confidence intervals or hypotheses tests.

Probability distribution and expectation . Although there is abundant research related to distribution, most of this research concentrates on data distribution or in sampling distribution. Another type of distribution is linked to the random variable, a powerful idea in probability, as well as the associated idea of expectation. Some probability distribution models in wide use are the binomial, uniform, and normal distributions.

Convergence and laws of large numbers . The progressive stabilization of the relative frequency of a given outcome in a large number of trials has been observed for centuries; Bernoulli proved the first version of the law of large numbers that justified the frequentist definition of probability. Today the frequentist approach, where probability is an estimate of the relative frequency of a result in a long series of trials, is promoted in teaching. It is important that students understand that each outcome is unpredictable and that regularity is only achieved in the long run. At the same time, older students should be able to discriminate between a frequency estimate (a value that varies) and probability (which is always a theoretical value) (Chaput et al. 2011 ).

Sampling and sampling distribution . Given that we are rarely able to study complete populations, our knowledge of a population is based on samples. Students are required to understand the ideas of sample representativeness and sampling variability. The sampling distributions describe the variation of a summary measure (e.g., sample means) along different samples from the same population. Instead of using the exact sampling distribution (e.g., a normal curve), teaching currently favours the use of simulation or re-sampling to find an empirical sampling distribution. This is a suitable teaching strategy, but teachers should be conscious that, as any estimate, the empirical sampling distribution only approximates the theoretical sampling distribution.

Modelling and simulation . Today we witness increasing recommendations to approach the teaching of probability from the point of view of modelling (Chaput et al. 2011 ; Eichler and Vogel 2014 ; Prodromou 2014 ). Simulation allows the exploration of probability concepts and properties, and is used in informal approaches to inference. Simulation acts as an intermediary step between reality and the mathematical model. As a didactic tool, it can serve to improve students’ probabilistic intuition, to acquire experience in the work of modelling, and to help students discriminate between model and reality.

2.4 Intuitions and Learning Difficulties

When teaching probability it is important to take into account the informal ideas that children and adolescents assign to chance and probability before instruction. These ideas are described in the breadth and depth of research investigating probabilistic intuitions, informal notions of probability, and resulting learning difficulties. Topics associated with teaching and learning probability, such as intuition, informal notions of probability, cognition, misconceptions, heuristics, knowledge, learning, reasoning, teaching, thinking, and understanding (among others), have developed over the last 60 years of research investigating probabilistic thinking (Chernoff and Sriraman 2014a ).

We now revisit the essentials associated with probabilistic intuition and difficulties associated with learning probability. Framing our historical approach, we adopt the periods of Jones and Thornton’s ( 2005 ) “historical overview of research on the learning and teaching of probability” (p. 66), which was recently extended by Chernoff and Sriraman ( 2014b ).

2.4.1 Piagetian and Post-piagetian Periods

Initial research in probability cognition was undertaken during the 1950s and 1960s by Piaget and Inhelder and by psychologists with varying theoretical orientations (Jones and Thornton 2005 ). Research during this period was dominated by the work of Piaget and Inhelder, Footnote 4 which largely investigated “developmental growth and structure of people’s probabilistic thinking” (p. 65). Extensive investigations would reveal that children in particular stages were prone to subjective intuitions (Piaget and Inhelder 1951/ 1975 ). Alternatively stated, research investigating intuition and learning difficulties was central at the beginnings of research in probabilistic thinking and would continue on into the next (historical) phase of research.

The next phase of research, the “Post-piagetian Period,” would be dominated, on the one hand, by work of Efraim Fischbein and, on the other hand, by Daniel Kahneman and Amos Tversky (Jones and Thornton 2005 ). The work of Fischbein would continue the work of Piaget and Inhelder (i.e., a continued focus on probabilistic intuitions), but introduce and explicate a distinction between what he denoted as primary and secondary intuitions. More specifically, Fischbein’s ( 1975 ) notion of primary intuitions (not associated with formal instruction) continued the work of Piaget and Inhelder’s research, but he differentiated his work during this period by investigating secondary intuitions (associated with formal instruction) and, further, how primary intuitions would not necessarily be overcome but rather replaced by secondary intuitions.

2.4.2 Heuristics and Biases Program

As mentioned, other investigations involving intuition were occurring in the field of psychology during this period, using different terminology. Footnote 5 Kahneman and Tversky’s original heuristics and biases program (see, for example, Kahneman et al. 1982 ), which became widely known (e.g., Kahneman 2011 ) and was revisited 20 years later (Gilovich et al. 2002 ), was, in essence, an in-depth investigation into intuitions (and learning difficulties).

Kahneman and Tversky’s research program investigated strategies that people used to calculate probabilities ( heuristics ) and the resultant systematic errors ( biases ). Their research revealed numerous heuristics (e.g., representativeness, availability and adjustment, and anchoring) and resulting biases. Years after generalising the notion of heuristics (Kahneman and Frederick 2002 ), Kahneman ( 2011 ) noted the essence of intuitive heuristics: “when faced with a difficult question, we often answer an easier one instead, usually without noticing the substitution” (p. 12). This research program played a key role in shaping many other fields of research (see, for example, behavioural economics).

In the field of mathematics education, the research of Shaughnessy ( 1977 , 1981 ) brought forth not only the theoretical ideas of Tversky and Kahneman, but also, in essence, research on probabilistic intuitions and learning difficulties. Although not explicitly deemed as intuitions and difficulties, work in this general area of research was conducted by a number of different individuals.

In particular, Falk’s ( 1981 ) research investigated difficulties associated with learning probability, and Konold ( 1989 , 1991 ) conducted research looking into informal conceptions of probability (most notably the outcome approach ). As the Post-piagetian Period came to a close, the field of mathematics education began to see an increasing volume of research on intuitions and learning difficulties (e.g., Green 1979 , 1983 , 1989 ; Fischbein and Gazit 1984 ), which is well summarised and synthesised in Shaughnessy’s ( 1992 ) extensive chapter on research in probability and statistics education. Moving from one period to the next, research into probabilistic intuitions and learning difficulties would come into its own during what Jones ( 2005 ) called Phase Three : Contemporary Research .

2.4.3 Contemporary Research

During this new phase there was, arguably, a major shift towards investigating curriculum and instruction, and the leadership of investigating probabilistic intuitions and learning difficulties was carried on by a particular group of researchers. Worthy of note, mathematics education researchers in this phase, as the case with Konold ( 1989 , 1991 ) and Falk ( 1981 ) in the previous phase, began to develop their own theories, frameworks, and models associated with responses to a variety of probabilistic tasks.

These theories, frameworks, and models were developed during research that investigated a variety of topics in probability, which included (difficulties associated with): randomness (e.g., Batanero et al. 2014 ; Batanero and Serrano 1999 ; Falk and Konold 1997 ; Pratt 2000 ), sample space (Jones et al. 1997 , 1999 ; Nunes et al. 2014 ), and probabilistic reasoning (Fischbein et al. 1991 ; Fischbein and Schnarch 1997 ; Lecoutre 1992 ; Konold et al. 1993 ). Worthy of note, the term misconceptio n, which acted as the de facto terminology for a number of years, has more recently evolved to preconceptions and other variants, which are perhaps better aligned with other theories in the field of mathematics education. In line with the above, research developing theories, models, and frameworks associated with intuition and learning difficulties continued into the next phase of research, which Chernoff and Sriraman ( 2014a ) have (prematurely) called the Assimilation Period.

After more than 50 years of research investigating probabilistic intuitions and difficulties associated with learning probability, the field of mathematics education has, in essence, come into its own, which is evidenced by the type of research being conducted and the manner in which results are presented. Gone are the early days where researchers were attempting to replicate research found in different fields, such as psychology (e.g., Shaughnessy 1977 , 1992 ). With that said, researchers are attempting to import theories, models, and frameworks from other fields; however, researchers in the field of mathematics education are forging their own interpretations of results stemming from the intuitive nature and difficulties associated with probability thinking and the teaching and learning of probability. Theories, models, and frameworks such as inadvertent metonymy (Abrahamson 2008 , 2009 ), sample space partitions (Chernoff 2009 , 2012a , b ), and others demonstrate that research into intuitions and difficulties continues in the field of mathematics education.

This does not mean, however, that the field does not continue to look to other domains of research to help better inform mathematics education. For example, recent investigations (e.g., Chernoff 2012a , b ) have gone back to their proverbial roots and integrated recent developments to the heuristics and biases program, which attempts to deal with the “arrested development of the representativeness heuristic in the field of mathematics education” (Chernoff 2012a , p. 951). Similar investigations embracing research from other fields have opened the door to alternative views of heuristics, intuitions, and learning difficulties, such as in the work by Gigerenzer and the Adaptive Behavior and Cognition (ABC) Group at the Max Planck Institute for Human Development in Berlin (e.g., Gigerenzer et al. 2011 ).

Based on these developments, the field of mathematics education is starting to also develop particular research which is building upon and questioning certain aspects of probabilistic intuitions and learning difficulties. For example, Chernoff, in a recent string of studies (e.g., Chernoff 2012a , b ; Chernoff and Zazkis 2011 ), has begun to establish that perhaps normatively incorrect responses to a variety of probabilistic tasks are best accounted for not by heuristics or informal reasoning, but rather participants’ use of logical fallacies.

In considering how students reason about probability, advances in technology and other educational resources have allowed for another important area of research, as described in the next section.

2.5 Technology and Educational Resources

Many educational resources have been used to support probability education. Some of the most common resources include physical devices such as dice, coins, spinners, marbles in a bag, and a Galton board that help create game-like scenarios that involve chance (Nilsson 2014 ). These devices are often used to support a classical approach to probability for computing the probability of an event occurring a priori by examining the object and making assumptions about symmetry that often lead to equiprobable outcomes for a single trial. When used together (e.g., two coins, a die, and a four-section spinner) these devices can be used to explore compound events and conditional probabilities (e.g., Martignon and Krauss 2009 ). Organizational tools such as two-by-two tables and tree diagrams are also used to assist in enumerating sample spaces (Nunes et al. 2014 ) and computing probabilities and can serve as important educational resources for students.

Since physical devices can also be acted upon, curriculum resources and teachers have increased the use of experiments with these devices to induce chance events (e.g., by rolling, spinning, choosing, or dropping a marble), often using relatively small sample sizes and recording frequencies of events. These frequencies and relative frequencies are used as an estimate of probability in the frequentist perspective, then often compared to the a priori computed probability based on examination of the object. Research by Nilsson ( 2007 , 2009 ), for example, provides insights into students’ thinking when engaged with experiments with such physical devices. Depending on the teachers’ or the students’ perspective, these experiments may favour one estimate of probability over another and issues related to sample size and the law of large numbers, or the difference between frequency and probability may or may not be discussed (Stohl 2005 ).

Many researchers (e.g., Chaput et al. 2011 ; Eicher and Vogel 2014 ; Lee and Lee 2011 ; Pratt 2011 ; Pratt and Ainley 2014 ; Prodromou 2014 ), and some curricula (e.g., CCSSI 2010 ; Raoult 2013 ), have recently emphasised that probability be taught as a way to model real-world phenomena rather than merely as an abstract measurement of something unseen about a real physical object (e.g., measure of likelihood of landing on heads when a coin is tossed). The sentiment is expressed by Pratt ( 2011 ):

Of course, if the modelling meaning of probability was stressed in the curriculum, it is debatable whether there is much advantage in maintaining the current emphasis on coins, spinners, dice and balls drawn from a bag. Perhaps, in days gone by when children played board games, there was some natural relevance in such contexts but, now that games take place in real time on screens, probability has much more relevance as a tool for modelling computer-based action and for simulating real-world events and phenomena (p. 892).

One way to help students use probability to model real-world phenomena is to engage the necessity to make a model explicit when using technology. In Biehler’s ( 1991 ) insightful comments on how technology should be used in probability education, he recommended several ways technology could advance learning and teaching probability. Sampling, storing, organising, and analysing data generated from a probabilistic model are facilitated tremendously by technology. These recommendations have been used by many researchers and have recently been made explicit for recommendations for teachers by Lee and Lee ( 2011 ) and for researchers by Pratt and Ainley ( 2014 ) and Pratt et al. ( 2011a , b ).

Accordingly, we still need to make substantial progress to investigate how students’ learning of probability models can be supported by the affordances of technology tools that will be used to frame the remaining discussion in the next sections.

2.5.1 Replicating Trials and Storing Data

One major contribution of technology to the study of probability is the ability to generate a large sample of data very quickly, store data in raw form as a sequence of outputs or organised table of frequencies, and collapse data into various aggregate representations. At times, the number of trials to perform is dictated by a teacher/researcher because of a pedagogical goal in mind; however, at other times, the number of trials is left open to be chosen by students.

Several researchers have discussed what students notice about sample size, particularly when they are able to examine its impact on variability in data distributions (e.g., Lee and Lee 2009 ; Lee et al. 2010 ; Pratt 2000 ). The ability of technology tools such as Probability Explorer or Fathom to store long lists of data sequences can also afford opportunities for students to examine a history of outcomes in the order in which they occurred, as well as conveniently collapsed in frequency and relative frequency tables and graphs.

2.5.2 Representing and Analysing Data

Technology tools bring real power to classrooms by allowing students to rapidly generate a large amount of data, quickly create tabular and graphical representations, and perform computations on data with ease. Students can then spend more time focused on making sense of data in various representations. Different representations of data in aggregate form can afford different perspectives on a problem. In addition, technology facilitates quickly generating, storing, and comparing multiple samples, each consisting of as many trials as desired. Instead of having each student in a class collect a small amount of data and then pool the data to form a class aggregate, students (or small groups) can generate individual samples of data, both small and large, and engage in reasoning about their own data as well as contribute to class discussions that examine results across samples (Stohl and Tarr 2002 ).

Technology can also provide opportunities for students to make sense of how an empirical distribution changes as data is being collected . This dynamic view of a distribution can assist students in exploring the relationship between a probability model and a resulting empirical distribution and how sample size impacts the variability observed (Drier 2000 ; Pratt et al. 2011a , b ). This relies upon intuitions about laws of large numbers; such intuitions may be strengthened by observing the settling down of relative frequency distributions as trials are simulated and displayed in real time. This type of work provides promising tasks and technology tools as well as future directions for how we can build on this work to better understand students’ reasoning with such dynamic representations.

2.5.3 Probability Technological Models

It is important to investigate the opportunities that technology affords for teachers and students to discuss explicitly the assumptions needed to build models to describe real-world scenarios through simulation. The model-building process should include discussing the pertinent characteristics of a situation being modelled, while in the same way simplifying reality (Chaput et al. 2011 ; Eichler and Vogel 2014 ). In the next steps, creating a mathematical model and working with it, the student should find ways to partition the events in which the probabilities are easily identifiable, using physical “chance makers” to model the random processes if possible and building and working with a simulated model with technological tools. Such steps are opportunities for students to grow in their understandings of a situation, the model, and many probability ideas. Using various technology tools (e.g., a graphing calculator, spreadsheet, or software such as Fathom or TinkerPlots) to create simulations for the same situation can force students to consider carefully how different commands in a tool can be used to create a model for a situation. Further, this can afford opportunities for discussing why two different ways of modelling a situation may be similar or different and differentiating between model and reality.

The modelling process may be as “simple” as having students design a discrete probability distribution that models a real spinner with three unequal sectors (e.g., Stohl and Tarr 2002 ) or designing a working model to consider whether larger families tend to either have more girls or more boys rather than the same number of boys and girls (Lee and Lee 2011 ). Modelling may also be as complex as interpreting medical information using input probabilities from real-life scenarios such as success or complications from back surgery to help a patient make an important life decision (e.g., Pratt et al. 2011a , b ).

Several tasks and tools discussed by Prodromou ( 2014 ) and Pratt and Ainley ( 2014 ) illustrate the importance of the ability to adjust parameters in a model-building and model-fitting process. The ability to easily adjust parameters in a model can afford many opportunities for students to explore “what if” scenarios. It allows for a process of model development, data generation and analysis, and model adjustment. Konold and Kazak ( 2008 ), for example, described how this process helped students in creating and modifying models based on how well a particular model behaved when a simulation was run.

2.5.4 Hiding a Model

Engaging with probability models and the data generated from such models can provide very important foundations for how probability is used in statistics, particularly in making inferences about populations and testing hypotheses. In the above cases, the models used in a simulation are typically created by students or created by a teacher but open for inspection by students. However, technology tools afford the ability to hide a model from the user such that underlying probability distributions that control a simulation are unknowable. These “black-box” types of simulations may assist students in thinking about probability from a subjective or frequentist perspective where they can only use data generated from a simulation to make estimates of probabilities that they can use in inference or decision-making situations. One example of such inference and decision-making situations can be found in the work of Lee et al. ( 2010 ) where 11- and 12-year-olds investigate whether a die company produces fair dice to make a decision about whether to buy dice from the company for a board game.

In summary, technology provides a big opportunity for probability education but also sets some challenges. One of them is the education of teachers to teach probability in general and to use technology in their teaching of probability in particular. We deal with this specific issue in the last section of our survey.

2.6 Education of Teachers

A consequence of the philosophical debates around the meaning of probability, the particular features of probabilistic reasoning, the students’ misconceptions and difficulties, and the increasing variety of technological resources is that teachers need specific preparation to teach probability. Although school textbooks provide examples and teaching resources, some texts present too narrow a view of probabilistic concepts or only one approach to probability. The applications of probability in textbooks may be restricted to games of chance and/or the definitions of concepts may be incorrect or incomplete (Cañizares et al. 2002 ).

Research in this area is scarce and is mostly focussed on the evaluation of prospective teachers’ knowledge of probability (e.g., Batanero et al. 2014 ; Chernoff and Russel 2012 ). While there is still need for further research into prospective and practising teacher probability knowledge, two important missing areas of research in probability education are the analysis of the components of teachers’ knowledge and the design of adequate materials and effective activities for educating teachers.

2.6.1 Components in Teacher Knowledge

Existent models of the knowledge needed by teachers in mathematics education, such as mathematical knowledge for teaching (MKT; Ball et al. 2008 ), suggest that teachers need different types of content and pedagogical knowledge. However, as stated by Godino et al. ( 2011 ) and Groth and Bergner ( 2013 ), for the particular case of statistical knowledge for teaching (SKT) it is important to recognise that teachers need content-specific knowledge to guide instruction. This means that any discussion of probability knowledge for teaching (PKT) should be supported in the specific features of probability.

First, teachers need adequate probabilistic knowledge. However, even if prospective teachers have a degree in mathematics, they have usually only studied theoretical probability and lack experience in designing investigations or simulations to work with students (Kvatinsky and Even 2002 ; Stohl 2005 ). The education of primary school teachers is even more challenging, because few of them have had suitable training in either theoretical or applied probability (Franklin and Mewborn 2006 ). Moreover, recent research suggests that many prospective teachers share with their students common biases in probabilistic reasoning (e.g., Batanero et al. 2014 ; Prodromou 2012 )

A second component is the pedagogical knowledge needed to teach probability, where general principles valid for other areas of mathematics are not always appropriate (Batanero et al. 2004 ). For example, in arithmetic or geometry, elementary operations can be reversed, and this reversibility can be represented by concrete materials, which serve to organise experiences where children progressively abstract the structure behind the concrete situation. The lack of reversibility in random experiences makes it more difficult for children to grasp the essential features of randomness, which may explain why they do not always develop correct probabilistic intuitions without a specific instruction.

In addition to the above, probability is difficult to teach because the teacher should not only present different probabilistic concepts and their applications but be aware of the different meanings of probability and philosophical controversies around them (Batanero et al. 2004 ). Finally, teachers should be acquainted with research results that describe children’s reasoning and beliefs in uncertain situations and with didactic materials that can help their students develop correct intuitions in this field.

The current use of technology warrants special considerations in the education of teachers that should be analysed. Lee and Hollebrands ( 2011 ) introduced a framework to describe what they call technological pedagogical statistical knowledge (TPSK) with examples of components in this knowledge. The evaluation and development of components in this framework for the specific case of probability is a promising research area.

2.6.2 Effective Ways to Train Teachers

Another line of research is designing and evaluating suitable and effective tasks that help in increasing the probabilistic and didactic knowledge of teachers. Some researchers describe different experiences directed towards achieving this goal.

Teachers should engage with and analyse probability simulations and investigations. Simulations and experiments are recommended when working with students. To be able to use investigations in their own classrooms, teachers need competencies with this approach to teaching. When the time available for educating teachers is scarce, one possibility is to give teachers first a project or investigation to work with and, when finished, carry out a didactical analysis of the project. This type of analysis can help to simultaneously increase the teachers’ mathematical and pedagogical knowledge (Batanero et al. 2004 ).

Teachers should engage with case discussions. Groth and Xu ( 2011 ) used case discussion among a group of teachers as a valuable strategy to educate teachers. The authors indicated that in teaching stochastics teachers navigate between two layers of uncertainty. On the one hand, uncertainty is part of stochastic knowledge; on the other hand, in any classroom uncertainty appears as a result of the dynamic interactions amongst teacher, students, and the topic being taught. Discussions among the teachers may help them to increase their knowledge since experiences with general pedagogy, mathematical content, and content-specific pedagogy can be offered and debated.

Teachers also need experience planning and analysing a lesson. When teachers plan and then analyse a lesson devised to teach some content they develop their probabilistic and professional knowledge (Chick and Pierce 2008 ). Teachers need to understand the probability they teach to their students. One strategy is to have teachers play the role of a learner and afterwards analyse what they learnt. If they have the chance to go through a lesson as a learner and at the same time look at it from the point a view of a teacher, they may understand better how the lesson will unfold later in the classroom.

Teachers should have extensive experience working with technology. We can also capitalise on technology as a tool-builder for teachers gaining a conceptual understanding of probabilistic ideas. Lee and Hollebrands ( 2011 ) describe the way technology can function both as amplifiers and reorganisers of teachers’ knowledge. They also discuss how technology can provide teachers with first-hand experience about how these tools can be useful in improving their stochastic thinking and knowledge. Other examples describe experiences and courses specifically directed to train teachers to teach probability or suggestions of how this training should be (e.g., Batanero et al. 2005a , b ; Dugdale 2001 ; Kvatinsky and Even 2002 ; Stohl 2005 ).

Research and development in teacher education related to probability education is still scarce and needs to be fostered.

3 Summary and Looking Ahead

In the previous sections we analysed the multifaceted nature of probability, the probabilistic contents in curricula, research dealing with intuitions and misconceptions, the role of technology, and the education of teachers. To finish this survey we suggest some points where new research is needed.

Different views on probability : As discussed in Sect.  2.1 , the different views of probability are linked to philosophical debates, and the school curricula at times has given too much emphasis to only one probability view. Since different views of probability are complementary (Henry 2010 ), reducing teaching to just one approach may explain some learning difficulties, as students may consider or apply only one interpretation in situations where it is inappropriate. Some research questions on this topic include: (a) an analysis of the particular views of probability implicit in curricular documents and textbooks for different school levels, (b) an exploration and consequent recommendations about the best age at which a particular view of probability should be introduced to students and about the best sequence to introduce different approaches to probability, (c) the design and evaluation of curricular guidelines for different ages that take into account each particular view of probability, and (d) the analyses of teachers’ educational needs in relation to each particular view of probability.

Probabilistic thinking and reasoning : Our analysis in Sect.  2.2 suggests that probabilistic reasoning complements logical, causal, and statistical reasoning. Consequently, the teaching of probabilistic thinking is important and justified in its own right and not simply as a tool to pave the way to inferential methods of statistics. Important research problems in this regard are: (a) clarifying the way in which probabilistic thinking could contribute to improving mathematical competencies of students, (b) analysing how different probability models and their applications can be presented to the students, (c) finding ways in which it is possible to engage students in questions related to how to obtain knowledge from data and why a probability model is suitable, and (d) how to help students develop valid intuitions in this field.

Probability in school curricula : Another important area of research is to enquire about how the fundamental ideas of probability have been reflected in school curricula at different levels and in different countries. The presentation of these ideas in textbooks for different curricular levels should also been taken into account (following previous research, e.g., Azcárate et al. 2006 ; Jones and Tarr 2007 ). We also need to find different levels of formalisation to teach each of these ideas depending on age and previous knowledge of students. Consequently, it is important to reflect on the main ideas that students should acquire at different ages, appropriate teaching methods, and suitable teaching situations.

Students ’ intuitions and learning difficulties : As suggested in previous research, probabilistic intuitions and difficulties in learning probability, albeit described in a variety of different forms, are a mainstay of research in psychology and mathematics education. Further, as the field grows and diversifies, there is reason to expect that this particular thread of research will not only continue but also grow. Important research questions in this area are: (a) describing primary school children’s preconceptions and intuitions in relation to new probability content in school curricula, (b) analysing changes in students’ intuitions about different probability concepts after specific teaching experiments, and (c) how “best” to account for preconceptions and difficulties.

Technology and education of teachers : The quick changes in technological development suggest a need for new research on students’ use of technology to solve real problem scenarios that use probability models. We need to know more about how students construct models and how they reason with data generated from such models. It is also important to evaluate the impact of technology on recent curricula and on the education of teachers. There is also a need for more systematic research about how teachers and students use technology in classrooms and how large-scale assessment should respond to capture new meanings for probability that may emerge from students working with probability using technology tools.

In conclusion, in this brief survey we have tried to summarise the extensive research in probability education. At the same time we intended to convince our readers of the need for new research and the many different ideas that still need to be investigated. We hope to have achieved these goals and look forward to new research in probability education.

Given \( \varepsilon > 0,\;\alpha > 0 \) arbitrarily small, the theorem establishes that for \( n > \frac{pq}{{\varepsilon \alpha^{2} }} \) , with q = 1−p

The sample space may be finite, countably infinite or uncountably infinite. The sample space is countably infinite when it can be put in correspondence with the set N of natural numbers.

For finite or countably infinite sample spaces S , A includes all subsets of S. For finite sample spaces A is a Boolean Algebra; in case of a countably infinite sample space, A is a σ-algebra, that is, it is closed under countable union and intersection operations and complement building. For uncountable (continuous) infinite sample spaces, the set algebra considered to assign probability does not include all possible subsets of S ; A is restricted instead to a system of events of S , closed under countable union and intersection operations and forming complements (Chung 2001 ).

To such an extent that Jones and Thornton denoted this period of research as “Piagetian Period.”

The theoretical constructs adopted by Daniel Kahneman and Amos Tversky differed from those of Fischbein and colleagues (e.g., Fischbein et al. 1970 ) and Piaget and Inhelder.

Abrahamson, D. (2008). Bridging theory: Activities designed to support the grounding of outcome-based combinatorial analysis in event-based intuitive judgment-A case study. In M. Borovcnik & D. Pratt (Eds.), Proceedings of Topic Study Group 13 at the 11th International Conference on Mathematics Education (ICME). Monterrey, Mexico. http://edrl.berkeley.edu/pubs/Abrahamson-ICME11-TSG13_BridgingTheory.pdf .

Abrahamson, D. (2009). Orchestrating semiotic leaps from tacit to cultural quantitative reasoning: the case of anticipating experimental outcomes of a quasi-binomial random generator. Cognition and Instruction, 27 (3), 175–224.

Article   Google Scholar  

Australian Curriculum, Assessment and Reporting Authority (ACARA) (2010). The Australian curriculum: Mathematics. Sidney, NSW: Author. http://www.australiancurriculum.edu.au/mathematics/curriculum/f-10?layout=1 .

Azcárate, P., Cardeñoso, J. M., & Serradó, S. (2006). Randomness in textbooks: the influence of deterministic thinking. In M. Bosch (Ed.), Proceedings of the Fourth Conference of the European Society for Research in Mathematics Education . Sant Feliu de Guixols, Spain: ERME. http://fractus.uson.mx/Papers/CERME4/Papers%20definitius/5/SerradAzcarCarde.pdf .

Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching. Journal of Teacher Education, 59 (5), 389–407.

Batanero, C. (2013). Teaching and learning probability. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 491–496). Heidelberg: Springer.

Google Scholar  

Batanero, C. (2015). Understanding randomness: Challenges for research and teaching. Plenary lecture. Ninth European Conference of Mathematics Education. Prague, Czech Republic.

Batanero, C., Arteaga, P., Serrano, L., & Ruiz, B. (2014). Prospective primary school teachers’ perception of randomness. In E. Chernoff & B. Sriraman (Eds.), Probabilistic thinking: Presenting plural perspectives (pp. 345–366). New York: Springer.

Chapter   Google Scholar  

Batanero, C., Biehler, R., Maxara, C., Engel, J., & Vogel, M. (2005a). Using simulation to bridge teachers’ content and pedagogical knowledge in probability. Paper presented at the fifteenth ICMI Study Conference: The professional education and development of teachers of mathematics. Aguas de Lindoia, Brazil: International Commission for Mathematical Instruction.

Batanero, C., & Díaz, C. (2007). Meaning and understanding of mathematics. The case of probability. In J. P Van Bendegen & K. François (Eds), Philosophical dimensions in mathematics education (pp. 107–127). New York: Springer.

Batanero, C., Godino, J. D., & Roa, R. (2004). Training teachers to teach probability. Journal of Statistics Education, 12. http://www.amstat.org/publications/jse/v12n1/batanero.html .

Batanero, C., Henry, M., & Parzysz, B. (2005b). The nature of chance and probability. In G. A. Jones (Ed.), Exploring probability in school: challenges for teaching and learning (pp. 15–37). New York: Springer.

Batanero, C., & Serrano, L. (1999). The meaning of randomness for secondary school students. Journal for Research in Mathematics Education, 30 (5), 558–567.

Bennett, D. J. (1999). Randomness . Cambridge, MA: Harvard University Press.

Ben-Zvi, D., & Garfield, J. B. (Eds.). (2004). The challenge of developing statistical literacy, reasoning and thinking . Dordrecht, The Netherlands: Kluwer.

Bernoulli, J. (1987). Ars conjectandi, Rouen: IREM. (Original work published in 1713).

Biehler, R. (1991). Computers in probability education. In R. Kapadia & M. Borovcnik (Eds.), Chance encounters: Probability in education (pp. 169–211). Dordrecht, The Netherlands: Kluwer.

Borovcnik, M. (2005). Probabilistic and statistical thinking, In M. Bosch (Ed.), Proceedings of the Fourth Conference on European Research in Mathematics Education. Sant Feliu de Guissols, Spain: ERME. http://fractus.uson.mx/Papers/CERME4/Papers%20definitius/5/Borovcnik.pdf .

Borovcnick, M. (2011). Strengthening the role of probability within statistics curricula. In C. Batanero, G. Burrill, & C. Reading (Eds.) (2011). Teaching Statistics in School Mathematics- Challenges for Teaching and Teacher Education. A Joint ICMI/IASE Study (pp. 71–83). New York: Springer.

Borovcnik, M. (2012). Multiple perspectives on the concept of conditional probability. Avances de Investigación en Educación Matemática, 2, 5–27. http://www.aiem.es/index.php/aiem/article/view/32 .

Borovcnik, M., Bentz, H. J., & Kapadia, R. (1991). Empirical research in understanding probability. In R. Kapadia & M. Borovcnik (Eds.), Chance encounters: Probability in education (pp. 73–105). Dordrecht, The Netherlands: Kluwer.

Borovcnik, M., & Kapadia, R. (2014a). A historical and philosophical perspective on probability. In E. J Chernoff & B. Sriraman, (Eds.), Probabilistic thinking: presenting plural perspectives (pp. 7–34). New York: Springer.

Borovcnik, M., & Kapadia, R. (2014b). From puzzles and paradoxes to concepts in probability. In E. J. Chernoff & B. Sriraman (Eds.), Probabilistic thinking: presenting plural perspectives (pp. 35–73). New York: Springer.

Cañizares, M. J., Ortiz, J. J., Batanero, C., & Serrano, L. (2002). Probabilistic language in Spanish textbooks. In B. Phillips (Ed.), ICOTS-6 papers for school teachers (pp. 207–211). Cape Town: International Association for Statistical Education.

Cardano, G. (1961). The book on games of chances. New York: Holt, Rinehart & Winston (Original work published in 1663).

Carnap, R. (1950). Logical foundations of probability . Chicago: University of Chicago Press.

Chaput, B., Girard, J. C., & Henry, M. (2011). Frequentist approach: Modelling and simulation in statistics and probability teaching. In C. Batanero, G. Burrill, & C. Reading (Eds.), Teaching Statistics in school mathematics-challenges for teaching and teacher education (pp. 85–95). New York: Springer.

Chernoff, E. J. (2009). Sample space partitions: An investigative lens. Journal of Mathematical Behavior, 28 (1), 19–29.

Chernoff, E. J. (2012a). Logically fallacious relative likelihood comparisons: the fallacy of composition. Experiments in Education, 40 (4), 77–84.

Chernoff, E. J. (2012b). Recognizing revisitation of the representativeness heuristic: an analysis of answer key attributes. ZDM - The International Journal on Mathematics Education, 44 (7), 941–952.

Chernoff, E. J., & Russell, G. L. (2012). The fallacy of composition: Prospective mathematics teachers’ use of logical fallacies. Canadian Journal of Science, Mathematics and Technology Education, 12 (3), 259–271.

Chernoff, E. J. & Sriraman, B. (2014a). Introduction. In E. J. Chernoff & B. Sriraman (Eds.), Probabilistic thinking: presenting plural perspectives (pp. xv–xviii). New York: Springer.

Chernoff, E. J. & Sriraman, B. (2014b). Commentary on probabilistic thinking: presenting plural perspectives. In E. J. Chernoff & B. Sriraman (Eds.), Probabilistic thinking: presenting plural perspectives (pp. 721–728). New York: Springer.

Chernoff, E. J., & Zazkis, R. (2011). From personal to conventional probabilities: from sample set to sample space. Educational Studies in Mathematics, 77 (1), 15–33.

Chick, H. L., & Pierce, R. U. (2008). Teaching statistics at the primary school level: beliefs, affordances, and pedagogical content knowledge. In C. Batanero, G. Burrill, C. Reading, & A. Rossman (Eds.), Proceedings of the ICMI study 18 and IASE round table conference . International Commission on Mathematics Instruction and International Association for Statistical Education: Monterrey, Mexico.

Chung, K. L. (2001). A course in probability theory . London: Academic Press.

Common Core State Standards Initiative (CCSSI). (2010). Common Core State Standards for Mathematics . Washington, DC: National Governors Association for Best Practices and the Council of Chief State School Officers. http://www.corestandards.org/Math/ .

David, F. N. (1962). Games, gods and gambling . London: Griffin.

de Finetti, B. (1933). Sul concetto di probabilità [On the concept of probability]. Rivista Italiana di Statistica, Economia e Finanza, 5 , 723–747.

de Moivre, A. (1967). The doctrine of chances . New York: Chelsea (Original work published in 1718).

Drier, H. S. (2000). Children’s meaning-making activity with dynamic multiple representations in a probability microworld. In M. Fernandez (Ed.), Proceedings of the twenty-second annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 691–696). Tucson, AZ: North American Chapter of the International Group for the Psychology of Mathematics Education.

Dugdale, S. (2001). Pre-service teachers’ use of computer simulation to explore probability. Computers in the Schools, 17 (1–2), 173–182.

Eichler, A., & Vogel, M. (2014). Three approaches for modelling situations with randomness. In E. J. Chernoff & B. Sriraman (Eds.), Probabilistic thinking: Presenting plural perspectives (pp. 75–99). New York: Springer.

Engel, J., & Sedlmeier, P. (2005). On middle-school students’ comprehension of randomness and chance variability in data-. Zentralblatt Didaktik der Mathematik, 37 (3), 168–177.

Engel, J., Sedlmeier, P., & Worn, C. (2008). Modelling scatterplot data and the signal-noise metaphor: Towards statistical literacy for pre-service teachers. In C. Batanero, G. Burrill, C. Reading, & A. Rossman (Eds.), Proceedings of the ICMI study 18 and IASE round table conference . International Commission on Mathematics Instruction and International Association for Statistical Education: Monterrey, Mexico.

Falk, R. (1981). The perception of randomness. Proceedings of the fifth conference of the International Group for the Psychology of Mathematics Education (pp. 222–229). Grenoble, France: University of Grenoble.

Falk, R., & Konold, C. (1992). The psychology of learning probability. In F. S. Gordon & S. P. Gordon (Eds.), Statistics for the twenty-first century (pp. 151–164). Washington: Mathematical Association of America.

Falk, R., & Konold, C. (1997). Making sense of randomness: Implicit encoding as a basis for judgement. Psychological Review, 104 (2), 310–318.

Fine, T. L. (1971). Theories of probability. An examination of foundations . London: Academic Press.

Fischbein, E. (1975). The intuitive source of probability thinking in children . Dordrecht, The Netherlands: Reidel.

Book   Google Scholar  

Fischbein, E., & Gazit, A. (1984). Does the teaching of probability improve probabilistic intuitions? Educational Studies in Mathematics, 15 , 1–24.

Fischbein, E., Nello, M. S., & Marino, M. S. (1991). Factors affecting probabilistic judgments in children and adolescents. Educational Studies in Mathematics, 22 , 523–549.

Fischbein, E., Pampu, I., & Minzat, I. (1970). Comparison of ratios and the chance concept in children. Child Development, 41 , 377–389.

Fischbein, E., & Schnarch, D. (1997). The evolution with age of probabilistic, intuitively based misconceptions. Journal for Research in Mathematics Education, 28 , 96–105.

Franklin, C., & Mewborn, D. (2006). The statistical education of PreK-12 teachers: A shared responsibility. In G. Burrill (Ed.), NCTM 2006 Yearbook: Thinking and reasoning with data and chance (pp. 335–344). Reston, VA: National Council of Teachers of Mathematics.

Franklin, C., Kader, G., Mewborn, D., Moreno, J., Peck, R., Perry, M., et al. (2007). Guidelines for assessment and instruction in statistics education (GAISE) report: A Pre-K-12 curriculum framework . Alexandria, VA: American Statistical Association. http://www.amstat.org/Education/gaise/ .

Gal, I. (2005). Towards “probability literacy” for all citizens: Building blocks and instructional dilemmas. In G. A. Jones (Ed.), Exploring probability in school. Challenges for teaching and learning (pp. 39–63). Dordrecht, The Netherlands: Kluwer.

Gigerenzer, G., Hertwig, R., & Pachur, T. (2011). Heuristics: The Foundations of Adaptive Behavior . Oxford, MA: University Press.

Gillies, D. (2000). Varieties of propensities. British Journal of Philosophy of Science, 51 , 807–835.

Gilovich, T., Griffin, D., & Kahneman, D. (2002). Heuristics and biases: The psychology of intuitive judgment . New York: Cambridge University Press.

Godino, J. D., Ortiz, J. J., Roa, R., & Wilhelmi, M. R. (2011). Models for statistical pedagogical knowledge. In C. Batanero, G. Burrill, & C. Reading (Eds.), Teaching statistics in school mathematics-challenges for teaching and teacher education (pp. 271–282). New York: Springer.

Green, D. (1979). The chance and probability concepts project. Teaching Statistics, 1 (3), 66–71.

Green, D. (1983). School pupils’ probability concepts. Teaching Statistics, 5 (2), 34–42.

Green, D. R. (1989). Schools students’ understanding of randomness. In R. Morris (Ed.), Studies in mathematics education: The teaching of statistics (Vol. 7, pp. 27–39). Paris: UNESCO.

Groth, R. E., & Bergner, J. S. (2013). Mapping the structure of knowledge for teaching nominal categorical data analysis. Educational Studies in Mathematics, 83 , 247–265.

Groth, R. E., & Xu, S. (2011). Preparing teachers through case analyses. In C. Batanero, G. Burrill, & C. Reading (Eds.), Teaching statistics in school mathematics-challenges for teaching and teacher education (pp. 371–382). New York: Springer.

Hacking, I. (1975). The emergence of probability . Cambridge, MA: Cambridge University Press.

Heitele, D. (1975). An epistemological view on fundamental stochastic ideas. Educational Studies in Mathematics, 6 , 187–205.

Henry, M. (2010). Evolution de l’enseignement secondaire français en statistique et probabilities [Evolution of French secondary teaching in statistics and probability]. Statistique et Enseignement, 1 (1), 35–45.

Jones, J. L., & Tarr, J. E. (2007). An examination of the levels of cognitive demand required by probability tasks in middle grade mathematics textbooks. Statistics Education Research Journal, 6 (2), 4–27.

Jones, G. A., Langrall, C. W., Thornton, C. A., & Mogill, A. T. (1997). A framework for assessing and nurturing young children’s thinking in instruction. Educational Studies in Mathematics, 32 , 101–125.

Jones, G. A., Langrall, C. W., Thornton, C. A., & Mogill, A. T. (1999). Students’ probabilistic thinking in instruction. Journal for Research in Mathematics Education, 30 , 487–519.

Kahneman, D. (2011). Thinking fast and slow . New York: MacMillan.

Kahneman, D., Slovic, P., & Tversky, A. (1982). Judgment under uncertainty: Heuristics and biases . New York: Cambridge University Press.

Kahneman, D., & Frederick, S. (2002). Representativeness revisited: attribute substitution in intuitive judgement. In T. Gilovich, D. Griffin, & D. Kahneman (Eds.), Heuristics and biases: The psychology of intuitive judgment (pp. 49–81). New York: Cambridge University Press.

Keynes, J. M. (1921). A treatise on probability . New York: MacMillan.

Kolmogorov, A. (1950). Foundations of probability’s calculation. New York: Chelsea Publishing Company (Original work, published in 1933).

Konold, C. (1989). Informal conceptions of probability. Cognition and Instruction, 6 , 59–98.

Konold, C. (1991). Understanding students’ beliefs about probability. In E. Von Glasersfeld (Ed.), Radical constructivism in mathematics education (pp. 139–156). Dordrecht, The Netherlands: Kluwer.

Konold, C., & Kazak, S. (2008). Reconnecting data and chance.  Technology Innovations in Statistics Education , 2 (1). https://escholarship.org/uc/item/38p7c94v .

Konold, C., & Pollatsek, A. (2002). Data analysis as the search for signals in noisy processes. Journal for Research in Mathematics Education, 33 (4), 259–289.

Konold, C., Pollatsek, A., Well, A., Lohmeier, J., & Lipson, A. (1993). Inconsistencies in students’ reasoning about probability. Journal for Research in Mathematics Education, 24 (5), 392–414.

Kultusministerkonferenz (KMK). (2004). Bildungsstandards im Fach Mathematik für den mittleren Schulabschluss [Educational standards in mathematics for middle school]. Berlin: Author.

Kultusministerkonferenz (KMK) (2012). Bildungsstandards im Fach Mathematik für die Allgemeine Hochschulreife [Educational standards in mathematics for the general higher education]. Berlin: Author.

Kvatinsky, T., & Even, R. (2002). Framework for teacher knowledge and understanding of probability. In B. Phillips (Ed.), Proceedings of the sixth international conference on teaching statistics . International Statistical Institute: Voorburg, The Netherlands.

Laplace, P. S. (1986). Essai philosophique sur les probabilités [Philosophical essay on Probabilities]. Paris: Christian Bourgois (Original work, published in 1814).

Langrall, C. W., & Mooney, E. S. (2005). Characteristics of elementary school students’ probabilistic reasoning. In G. Jones (Ed.), Exploring probability in school (pp. 95–119). New York: Springer.

Lee, H. S., Angotti, R. L., & Tarr, J. E. (2010). Making comparisons between observed data and expected outcomes: Students’ informal hypothesis testing with probability simulation tools. Statistics Education Research Journal, 9 (1), 68–96.

Lee, H. S., & Hollebrands, K. F. (2011). Characterising and developing teachers’ knowledge for teaching statistics with technology. In C. Batanero, G. Burrill, & C. Reading (Eds.), Teaching statistics in school mathematics-challenges for teaching and teacher education (pp. 359–369). Netherlands: Springer.

Lee, H. S., & Lee, J. T. (2009). Reasoning about probabilistic phenomena: Lessons learned and applied in software design. Technology Innovations in Statistics Education 3 (2). https://escholarship.org/uc/item/1b54h9s9 .

Lee, H. S., & Lee, J. T. (2011). Simulations as a path for making sense of probability. In K. Hollebrands & T. Dick (Eds.), Focus in high school mathematics on reasoning and sense making with technology (pp. 69–88). Reston, VA: National Council of Teachers of Mathematics.

Lecoutre, M. (1992). Cognitive models and problem spaces in “purely random” situations. Educational Studies in Mathematics, 23 , 557–568.

Martignon, L. (2014). Fostering children’s probabilistic reasoning and first elements of risk evaluation In E. J. Chernoff, B. & Sriraman (Eds.), Probabilistic thinking, presenting plural perspectives (pp. 149–160). Dordrecht: The Netherlands: Springer.

Martignon, L., & Krauss, S. (2009). Hands on activities with fourth-graders: a tool box of heuristics for decision making and reckoning with risk. International Electronic Journal for Mathematics Education, 4 , 117–148.

Mellor, D. H. (1971). The matter of chance . Cambridge: Cambridge University Press.

Ministerio de Educación y Ciencia, MEC. (2006). Real Decreto 1513/2006, de 7 de diciembre, por el que se establecen las enseñanzas mínimas de la Educación Primaria [Royal Decree establishing the minimum content for Primary Education] Madrid: Author.

Ministerio de Educación y Ciencia, MEC. (2007a). Real Decreto 1631/2006, de 29 de diciembre, por el que se establecen las enseñanzas mínimas correspondientes a la Educación Secundaria Obligatoria [Royal Decree establishing the minimum content for Compulsory Secondary Education]. Madrid: Author.

Ministerio de Educación y Ciencia, MEC. (2007b). R eal Decreto 1467/2007, de 2 de noviembre, por el que se establece la estructura del bachillerato y se fijan sus enseñanzas mínimas [Royal Decree establishing the structure and minimum content for High School]. Madrid: Author.

Ministerio de Educación, Cultura y Deporte, MECD. (2014). Real Decreto 126/2014, de 28 de febrero, por el que se establece el currículo básico de la Educación Primaria [Royal Decree establishing the minimum content for Primary Education]. Madrid: Author.

Ministerio de Educación, Cultura y Deporte, MECD. (2015). Real Decreto 1105/2014, de 26 de diciembre, por el que se establece el currículo básico de la Educación Secundaria Obligatoria y del Bachillerato [Royal Decree establishing the minimum content for Compulsory Secondary Education and High School]. Madrid: Author.

Ministerio de Educación Pública, MEP. (2012). Programas de Estudio de Matemáticas [Study programs for mathematics]. San José: Costa Rica: Author.

Ministry of Education, ME. (2007). The New Zealand curriculum . Wellington, New Zealand: Learning Media.

Moore, D. S. (2010). The basic practice of statistics. New York: Freeman (5th edition).

National Council of Teachers of Mathematics, NCTM. (2000). Principles and standards for school mathematics. Reston, VA: Author.

Nilsson, P. (2007). Different ways in which students handle chance encounters in the explorative setting of a dice game. Educational Studies in Mathematics, 66 , 293–315.

Nilsson, P. (2009). Conceptual variation and coordination in probability reasoning. The Journal of Mathematical Behavior, 28 (4), 247–261.

Nilsson, P. (2014). Experimentation in probability teaching and learning. In E. Chernoff & B. Sriraman (Eds.), Probabilistic thinking. Presenting multiple perspectives (pp. 509–532). New York: Springer.

Nunes, T., Bryant, P., Evans, D., Gottardis, L., & Terlektsi, M. E. (2014). The cognitive demands of understanding the sample space. ZDM - The International Journal on Mathematics Education, 46 (3), 437–448.

Pange, J., & Talbot, M. (2003). Literature survey and children’s perception on risk. ZDM - The International Journal on Mathematics Education, 35 (4), 182–186.

Pascal, B. (1963). Correspondance avec Fermat [Correspondence with Fermat]. In B. Pascal, Oeuvres Complètes (pp. 43–49). París: Seuil (Original letter written in 1654).

Peirce, C. S. (1932). Notes on the doctrine of chances. In C. S. Peirce, Collected papers (Vol. 2, pp. 404–414). Havard University Press (Original work published in 1910).

Piaget, J., & Inhelder, B. (1975). The origin of the idea of chance in children . New York: Norton. (Original work published in 1951).

Popper, K. R. (1959). The propensity interpretation of probability. British Journal of the Philosophy of Science, 10 , 25–42.

Pratt, D. (2000). Making sense of the total of two dice. Journal for Research in mathematics Education, 31 (5), 602–625.

Pratt, D. (2011). Re-connecting probability and reasoning about data in secondary school teaching. Paper presented at 58th ISI World Statistics Congress , Dublin, Ireland. http://2011.isiproceedings.org/papers/450478.pdf .

Pratt, D., & Ainley, J. (2014). Chance re-encounters: Computers in probability education revisited. In T. Wassong (Ed.), Mit Werkzeugen mathematik und stochastik lernen–using tools for learning mathematics and statistics (pp. 165–177). Wiesbaden: Springer Fachmedien.

Pratt, D., Ainley, J., Kent, P., Levinson, R., Yogui, C., & Kapadia, R. (2011a). Role of context in risk-based reasoning. Mathematical Thinking and Learning , 13 (4), 322–345.

Pratt, D., Davies, N., & Connor, D. (2011b). The role of technology in teaching and learning statistics. In C. Batanero, G. Burrill, & C. Reading (Eds.). Teaching statistics in school mathematics-challenges for teaching and teacher education (pp. 97–107). New York: Springer.

Prodromou, T. (2012). Connecting experimental probability and theoretical probability. ZDM - The International Journal on Mathematics Education, 44 (7), 855–868.

Prodromou, T. (2014). Developing a modelling approach to probability Using computer-based simulations. In E. Chernoff & B. Sriraman (Eds.), Probabilistic thinking. Presenting multiple perspectives (pp. 417–439). New York: Springer.

Raoult, J. P. (2013). La statistique dans l’enseignement secondaire en France [Statistics in secondary teaching in France]. Statistique et Enseignement, 4 (1), 55–69. http://publications-sfds.fr/ojs/index.php/StatEns/article/view/138 .

Renyi, A. (1992). Calcul des probabilités [Probability calculus]. Paris: Jacques Gabay (Original work published 1966).

Savage, R. (1994). The paradox of nontransitive dice. American Mathematical Monthly, 101 (5), 429–436.

Senior Secondary Board of South Australia (SSBSA). (2002). Mathematical studies curriculum statement . Adelaide, Australia: SSBSA.

SEP. (2011). Plan de Estudios, Educación Básica . México: Secretaría de Educación Pública.

Shaughnessy, J. M. (1977). Misconceptions of probability: An experiment with a small-group, activity-based, model building approach to introductory probability at the college level. Educational Studies in Mathematics, 8 , 285–316.

Shaughnessy, J. M. (1981). Misconceptions of probability: From systematic errors to systematic experiments and decisions. In A. Schulte (Ed.), Teaching statistics and probability: Yearbook of the National Council of Teachers of Mathematics (pp. 90–100). Reston, VA: National Council of Teachers of Mathematics.

Stohl, H. (2005). Probability in teacher education and development. In G. Jones (Ed.), Exploring probability in schools: Challenges for teaching and learning (pp. 345–366). New York: Springer.

Stohl, H., & Tarr, J. E. (2002). Developing notions of inference with probability simulation tools. Journal of Mathematical Behavior, 21 (3), 319–337.

von Mises, R. (1952). Probability, statistics and truth . London: William Hodge. (Original work published in 1928).

Wassong, T., & Biehler, R. (2010). A model for teacher knowledge as a basis for online courses for professional development of statistics teachers. In C. Reading (Ed.), Proceedings of the 8th International Conference on Teaching Statistics . Lubjana, Slovenia: International Association for Statistical Education.

Wild, C., & Pfannkuch, M. (1999). Statistical thinking in empirical enquiry. International Statistical Review, 3 , 223–266.

Further reading

Batanero, C. (2013b). Teaching and learning probability. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 491–496). Heidelberg, Germany: Springer.

Borovcnik, M., & Peard, R. (1996). Probability. In A. Bishop, M.A. Clements, C. Keitel, J. Kilpatrick, & C. Laborde (Eds.), International handbook of mathematics education (pp. 239–288). Dordrecht: The Netherlands: Kluwer.

Chernoff, E. J., & Sriraman, B. (Eds.) (2014), Probabilistic thinking. Presenting multiple perspectives. New York: Springer.

Kapadia, R., & Borovcnik M. (Eds.) (1991). Chance encounters. Mathematics Education Library vol 12. Dordrecht: The Netherlands: Kluwer.

Jones, G. A. (2005). Exploring probability in schools. Challenges for teaching and learning. Mathematics Education Library vol 40 . New York: Springer.

Jones, G., Langrall, C., & Mooney, E. (2007). Research in probability: responding to classroom realities. In F. Lester (Ed.), Second handbook of research on mathematics teaching and learning . Greenwich, CT: Information Age Publishing and NCTM.

Jones, G. A., & Thornton, C. A. (2005). An overview of research into the learning and teaching of probability. In G. A. Jones (Ed.), Exploring probability in school: Challenges for teaching and learning (pp. 65–92). New York: Springer.

Shaughnessy, J. M. (1992). Research in probability and statistics: Reflections and directions. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 465–494). New York: Macmillan.

Shaughnessy, J. M. (2007). Research on statistics learning and reasoning. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 957–1009). Charlotte, NC: Information Age Publishing.

Author note: We appreciate the input from Juan D. Godino who gave critical feedback on this manuscript that greatly improved the final version. Financial support was provided by the Spanish Ministry of Economy and Competitivity (Project EDU2013-41141-P).

Download references

Author information

Authors and affiliations.

Facultad de Ciencias de la Educación, University of Granada, Granada, Spain

Carmen Batanero

College of Education, University of Saskatchewan, Saskatoon, SK, Canada

Egan J. Chernoff

Department of Mathematics and Computer Science, Ludwigsburg University of Education, Ludwigsburg, Germany

Joachim Engel

Department of Science, Technology, Engineering, and Mathematics Education, North Carolina State University, Raleigh, NC, USA

Hollylynne S. Lee

Departamento de Matemática Educativa, CINVESTAV-IPN, Mexico, Distrito Federal, Mexico

Ernesto Sánchez

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Carmen Batanero .

Rights and permissions

Open Access This chapter is distributed under the terms of the Creative Commons Attribution-NonCommercial 4.0 International License ( http://creativecommons.org/licenses/by-nc/4.0/ ), which permits any noncommercial use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.

The images or other third party material in this chapter are included in the work’s Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work’s Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.

Reprints and permissions

Copyright information

© 2016 The Author(s)

About this chapter

Batanero, C., Chernoff, E.J., Engel, J., Lee, H.S., Sánchez, E. (2016). Research on Teaching and Learning Probability. In: Research on Teaching and Learning Probability. ICME-13 Topical Surveys. Springer, Cham. https://doi.org/10.1007/978-3-319-31625-3_1

Download citation

DOI : https://doi.org/10.1007/978-3-319-31625-3_1

Published : 13 July 2016

Publisher Name : Springer, Cham

Print ISBN : 978-3-319-31624-6

Online ISBN : 978-3-319-31625-3

eBook Packages : Education Education (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base

The Beginner's Guide to Statistical Analysis | 5 Steps & Examples

Statistical analysis means investigating trends, patterns, and relationships using quantitative data . It is an important research tool used by scientists, governments, businesses, and other organizations.

To draw valid conclusions, statistical analysis requires careful planning from the very start of the research process . You need to specify your hypotheses and make decisions about your research design, sample size, and sampling procedure.

After collecting data from your sample, you can organize and summarize the data using descriptive statistics . Then, you can use inferential statistics to formally test hypotheses and make estimates about the population. Finally, you can interpret and generalize your findings.

This article is a practical introduction to statistical analysis for students and researchers. We’ll walk you through the steps using two research examples. The first investigates a potential cause-and-effect relationship, while the second investigates a potential correlation between variables.

Table of contents

Step 1: write your hypotheses and plan your research design, step 2: collect data from a sample, step 3: summarize your data with descriptive statistics, step 4: test hypotheses or make estimates with inferential statistics, step 5: interpret your results, other interesting articles.

To collect valid data for statistical analysis, you first need to specify your hypotheses and plan out your research design.

Writing statistical hypotheses

The goal of research is often to investigate a relationship between variables within a population . You start with a prediction, and use statistical analysis to test that prediction.

A statistical hypothesis is a formal way of writing a prediction about a population. Every research prediction is rephrased into null and alternative hypotheses that can be tested using sample data.

While the null hypothesis always predicts no effect or no relationship between variables, the alternative hypothesis states your research prediction of an effect or relationship.

• Null hypothesis: A 5-minute meditation exercise will have no effect on math test scores in teenagers.
• Alternative hypothesis: A 5-minute meditation exercise will improve math test scores in teenagers.
• Null hypothesis: Parental income and GPA have no relationship with each other in college students.
• Alternative hypothesis: Parental income and GPA are positively correlated in college students.

Planning your research design

A research design is your overall strategy for data collection and analysis. It determines the statistical tests you can use to test your hypothesis later on.

First, decide whether your research will use a descriptive, correlational, or experimental design. Experiments directly influence variables, whereas descriptive and correlational studies only measure variables.

• In an experimental design , you can assess a cause-and-effect relationship (e.g., the effect of meditation on test scores) using statistical tests of comparison or regression.
• In a correlational design , you can explore relationships between variables (e.g., parental income and GPA) without any assumption of causality using correlation coefficients and significance tests.
• In a descriptive design , you can study the characteristics of a population or phenomenon (e.g., the prevalence of anxiety in U.S. college students) using statistical tests to draw inferences from sample data.

Your research design also concerns whether you’ll compare participants at the group level or individual level, or both.

• In a between-subjects design , you compare the group-level outcomes of participants who have been exposed to different treatments (e.g., those who performed a meditation exercise vs those who didn’t).
• In a within-subjects design , you compare repeated measures from participants who have participated in all treatments of a study (e.g., scores from before and after performing a meditation exercise).
• In a mixed (factorial) design , one variable is altered between subjects and another is altered within subjects (e.g., pretest and posttest scores from participants who either did or didn’t do a meditation exercise).
• Experimental
• Correlational

First, you’ll take baseline test scores from participants. Then, your participants will undergo a 5-minute meditation exercise. Finally, you’ll record participants’ scores from a second math test.

In this experiment, the independent variable is the 5-minute meditation exercise, and the dependent variable is the math test score from before and after the intervention. Example: Correlational research design In a correlational study, you test whether there is a relationship between parental income and GPA in graduating college students. To collect your data, you will ask participants to fill in a survey and self-report their parents’ incomes and their own GPA.

Measuring variables

When planning a research design, you should operationalize your variables and decide exactly how you will measure them.

For statistical analysis, it’s important to consider the level of measurement of your variables, which tells you what kind of data they contain:

• Categorical data represents groupings. These may be nominal (e.g., gender) or ordinal (e.g. level of language ability).
• Quantitative data represents amounts. These may be on an interval scale (e.g. test score) or a ratio scale (e.g. age).

Many variables can be measured at different levels of precision. For example, age data can be quantitative (8 years old) or categorical (young). If a variable is coded numerically (e.g., level of agreement from 1–5), it doesn’t automatically mean that it’s quantitative instead of categorical.

Identifying the measurement level is important for choosing appropriate statistics and hypothesis tests. For example, you can calculate a mean score with quantitative data, but not with categorical data.

In a research study, along with measures of your variables of interest, you’ll often collect data on relevant participant characteristics.

Prevent plagiarism. Run a free check.

In most cases, it’s too difficult or expensive to collect data from every member of the population you’re interested in studying. Instead, you’ll collect data from a sample.

Statistical analysis allows you to apply your findings beyond your own sample as long as you use appropriate sampling procedures . You should aim for a sample that is representative of the population.

Sampling for statistical analysis

There are two main approaches to selecting a sample.

• Probability sampling: every member of the population has a chance of being selected for the study through random selection.
• Non-probability sampling: some members of the population are more likely than others to be selected for the study because of criteria such as convenience or voluntary self-selection.

In theory, for highly generalizable findings, you should use a probability sampling method. Random selection reduces several types of research bias , like sampling bias , and ensures that data from your sample is actually typical of the population. Parametric tests can be used to make strong statistical inferences when data are collected using probability sampling.

But in practice, it’s rarely possible to gather the ideal sample. While non-probability samples are more likely to at risk for biases like self-selection bias , they are much easier to recruit and collect data from. Non-parametric tests are more appropriate for non-probability samples, but they result in weaker inferences about the population.

If you want to use parametric tests for non-probability samples, you have to make the case that:

• your sample is representative of the population you’re generalizing your findings to.
• your sample lacks systematic bias.

Keep in mind that external validity means that you can only generalize your conclusions to others who share the characteristics of your sample. For instance, results from Western, Educated, Industrialized, Rich and Democratic samples (e.g., college students in the US) aren’t automatically applicable to all non-WEIRD populations.

If you apply parametric tests to data from non-probability samples, be sure to elaborate on the limitations of how far your results can be generalized in your discussion section .

Create an appropriate sampling procedure

Based on the resources available for your research, decide on how you’ll recruit participants.

• Will you have resources to advertise your study widely, including outside of your university setting?
• Will you have the means to recruit a diverse sample that represents a broad population?
• Do you have time to contact and follow up with members of hard-to-reach groups?

Your participants are self-selected by their schools. Although you’re using a non-probability sample, you aim for a diverse and representative sample. Example: Sampling (correlational study) Your main population of interest is male college students in the US. Using social media advertising, you recruit senior-year male college students from a smaller subpopulation: seven universities in the Boston area.

Calculate sufficient sample size

Before recruiting participants, decide on your sample size either by looking at other studies in your field or using statistics. A sample that’s too small may be unrepresentative of the sample, while a sample that’s too large will be more costly than necessary.

There are many sample size calculators online. Different formulas are used depending on whether you have subgroups or how rigorous your study should be (e.g., in clinical research). As a rule of thumb, a minimum of 30 units or more per subgroup is necessary.

To use these calculators, you have to understand and input these key components:

• Significance level (alpha): the risk of rejecting a true null hypothesis that you are willing to take, usually set at 5%.
• Statistical power : the probability of your study detecting an effect of a certain size if there is one, usually 80% or higher.
• Expected effect size : a standardized indication of how large the expected result of your study will be, usually based on other similar studies.
• Population standard deviation: an estimate of the population parameter based on a previous study or a pilot study of your own.

Once you’ve collected all of your data, you can inspect them and calculate descriptive statistics that summarize them.

Inspect your data

There are various ways to inspect your data, including the following:

• Organizing data from each variable in frequency distribution tables .
• Displaying data from a key variable in a bar chart to view the distribution of responses.
• Visualizing the relationship between two variables using a scatter plot .

By visualizing your data in tables and graphs, you can assess whether your data follow a skewed or normal distribution and whether there are any outliers or missing data.

A normal distribution means that your data are symmetrically distributed around a center where most values lie, with the values tapering off at the tail ends.

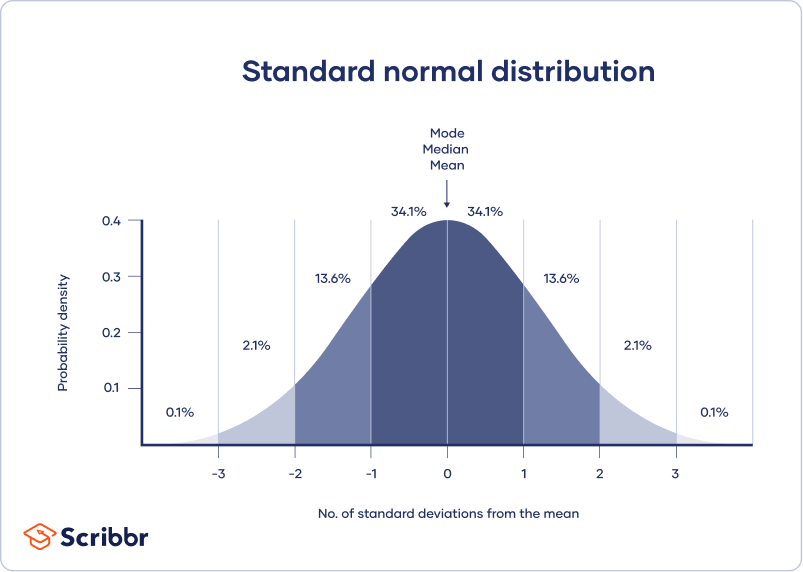
In contrast, a skewed distribution is asymmetric and has more values on one end than the other. The shape of the distribution is important to keep in mind because only some descriptive statistics should be used with skewed distributions.

Extreme outliers can also produce misleading statistics, so you may need a systematic approach to dealing with these values.

Calculate measures of central tendency

Measures of central tendency describe where most of the values in a data set lie. Three main measures of central tendency are often reported:

• Mode : the most popular response or value in the data set.
• Median : the value in the exact middle of the data set when ordered from low to high.
• Mean : the sum of all values divided by the number of values.

However, depending on the shape of the distribution and level of measurement, only one or two of these measures may be appropriate. For example, many demographic characteristics can only be described using the mode or proportions, while a variable like reaction time may not have a mode at all.

Calculate measures of variability

Measures of variability tell you how spread out the values in a data set are. Four main measures of variability are often reported:

• Range : the highest value minus the lowest value of the data set.
• Interquartile range : the range of the middle half of the data set.
• Standard deviation : the average distance between each value in your data set and the mean.
• Variance : the square of the standard deviation.

Once again, the shape of the distribution and level of measurement should guide your choice of variability statistics. The interquartile range is the best measure for skewed distributions, while standard deviation and variance provide the best information for normal distributions.

Using your table, you should check whether the units of the descriptive statistics are comparable for pretest and posttest scores. For example, are the variance levels similar across the groups? Are there any extreme values? If there are, you may need to identify and remove extreme outliers in your data set or transform your data before performing a statistical test.

From this table, we can see that the mean score increased after the meditation exercise, and the variances of the two scores are comparable. Next, we can perform a statistical test to find out if this improvement in test scores is statistically significant in the population. Example: Descriptive statistics (correlational study) After collecting data from 653 students, you tabulate descriptive statistics for annual parental income and GPA.

It’s important to check whether you have a broad range of data points. If you don’t, your data may be skewed towards some groups more than others (e.g., high academic achievers), and only limited inferences can be made about a relationship.

A number that describes a sample is called a statistic , while a number describing a population is called a parameter . Using inferential statistics , you can make conclusions about population parameters based on sample statistics.

Researchers often use two main methods (simultaneously) to make inferences in statistics.

• Estimation: calculating population parameters based on sample statistics.
• Hypothesis testing: a formal process for testing research predictions about the population using samples.

You can make two types of estimates of population parameters from sample statistics:

• A point estimate : a value that represents your best guess of the exact parameter.
• An interval estimate : a range of values that represent your best guess of where the parameter lies.

If your aim is to infer and report population characteristics from sample data, it’s best to use both point and interval estimates in your paper.

You can consider a sample statistic a point estimate for the population parameter when you have a representative sample (e.g., in a wide public opinion poll, the proportion of a sample that supports the current government is taken as the population proportion of government supporters).

There’s always error involved in estimation, so you should also provide a confidence interval as an interval estimate to show the variability around a point estimate.

A confidence interval uses the standard error and the z score from the standard normal distribution to convey where you’d generally expect to find the population parameter most of the time.

Hypothesis testing

Using data from a sample, you can test hypotheses about relationships between variables in the population. Hypothesis testing starts with the assumption that the null hypothesis is true in the population, and you use statistical tests to assess whether the null hypothesis can be rejected or not.

Statistical tests determine where your sample data would lie on an expected distribution of sample data if the null hypothesis were true. These tests give two main outputs:

• A test statistic tells you how much your data differs from the null hypothesis of the test.
• A p value tells you the likelihood of obtaining your results if the null hypothesis is actually true in the population.

Statistical tests come in three main varieties:

• Comparison tests assess group differences in outcomes.
• Regression tests assess cause-and-effect relationships between variables.
• Correlation tests assess relationships between variables without assuming causation.

Your choice of statistical test depends on your research questions, research design, sampling method, and data characteristics.

Parametric tests

Parametric tests make powerful inferences about the population based on sample data. But to use them, some assumptions must be met, and only some types of variables can be used. If your data violate these assumptions, you can perform appropriate data transformations or use alternative non-parametric tests instead.

A regression models the extent to which changes in a predictor variable results in changes in outcome variable(s).

• A simple linear regression includes one predictor variable and one outcome variable.
• A multiple linear regression includes two or more predictor variables and one outcome variable.

Comparison tests usually compare the means of groups. These may be the means of different groups within a sample (e.g., a treatment and control group), the means of one sample group taken at different times (e.g., pretest and posttest scores), or a sample mean and a population mean.

• A t test is for exactly 1 or 2 groups when the sample is small (30 or less).
• A z test is for exactly 1 or 2 groups when the sample is large.
• An ANOVA is for 3 or more groups.

The z and t tests have subtypes based on the number and types of samples and the hypotheses:

• If you have only one sample that you want to compare to a population mean, use a one-sample test .
• If you have paired measurements (within-subjects design), use a dependent (paired) samples test .
• If you have completely separate measurements from two unmatched groups (between-subjects design), use an independent (unpaired) samples test .
• If you expect a difference between groups in a specific direction, use a one-tailed test .
• If you don’t have any expectations for the direction of a difference between groups, use a two-tailed test .

The only parametric correlation test is Pearson’s r . The correlation coefficient ( r ) tells you the strength of a linear relationship between two quantitative variables.

However, to test whether the correlation in the sample is strong enough to be important in the population, you also need to perform a significance test of the correlation coefficient, usually a t test, to obtain a p value. This test uses your sample size to calculate how much the correlation coefficient differs from zero in the population.

You use a dependent-samples, one-tailed t test to assess whether the meditation exercise significantly improved math test scores. The test gives you:

• a t value (test statistic) of 3.00
• a p value of 0.0028

Although Pearson’s r is a test statistic, it doesn’t tell you anything about how significant the correlation is in the population. You also need to test whether this sample correlation coefficient is large enough to demonstrate a correlation in the population.

A t test can also determine how significantly a correlation coefficient differs from zero based on sample size. Since you expect a positive correlation between parental income and GPA, you use a one-sample, one-tailed t test. The t test gives you:

• a t value of 3.08
• a p value of 0.001

Receive feedback on language, structure, and formatting

Professional editors proofread and edit your paper by focusing on:

• Academic style
• Vague sentences
• Style consistency

See an example

The final step of statistical analysis is interpreting your results.

Statistical significance

In hypothesis testing, statistical significance is the main criterion for forming conclusions. You compare your p value to a set significance level (usually 0.05) to decide whether your results are statistically significant or non-significant.

Statistically significant results are considered unlikely to have arisen solely due to chance. There is only a very low chance of such a result occurring if the null hypothesis is true in the population.

This means that you believe the meditation intervention, rather than random factors, directly caused the increase in test scores. Example: Interpret your results (correlational study) You compare your p value of 0.001 to your significance threshold of 0.05. With a p value under this threshold, you can reject the null hypothesis. This indicates a statistically significant correlation between parental income and GPA in male college students.

Note that correlation doesn’t always mean causation, because there are often many underlying factors contributing to a complex variable like GPA. Even if one variable is related to another, this may be because of a third variable influencing both of them, or indirect links between the two variables.

Effect size

A statistically significant result doesn’t necessarily mean that there are important real life applications or clinical outcomes for a finding.

In contrast, the effect size indicates the practical significance of your results. It’s important to report effect sizes along with your inferential statistics for a complete picture of your results. You should also report interval estimates of effect sizes if you’re writing an APA style paper .

With a Cohen’s d of 0.72, there’s medium to high practical significance to your finding that the meditation exercise improved test scores. Example: Effect size (correlational study) To determine the effect size of the correlation coefficient, you compare your Pearson’s r value to Cohen’s effect size criteria.

Decision errors

Type I and Type II errors are mistakes made in research conclusions. A Type I error means rejecting the null hypothesis when it’s actually true, while a Type II error means failing to reject the null hypothesis when it’s false.

You can aim to minimize the risk of these errors by selecting an optimal significance level and ensuring high power . However, there’s a trade-off between the two errors, so a fine balance is necessary.

Frequentist versus Bayesian statistics

Traditionally, frequentist statistics emphasizes null hypothesis significance testing and always starts with the assumption of a true null hypothesis.

However, Bayesian statistics has grown in popularity as an alternative approach in the last few decades. In this approach, you use previous research to continually update your hypotheses based on your expectations and observations.

Bayes factor compares the relative strength of evidence for the null versus the alternative hypothesis rather than making a conclusion about rejecting the null hypothesis or not.

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Student’s  t -distribution
• Normal distribution
• Null and Alternative Hypotheses
• Chi square tests
• Confidence interval

Methodology

• Cluster sampling
• Stratified sampling
• Data cleansing
• Reproducibility vs Replicability
• Peer review
• Likert scale

Research bias

• Implicit bias
• Framing effect
• Cognitive bias
• Placebo effect
• Hawthorne effect
• Hostile attribution bias
• Affect heuristic

Is this article helpful?

Other students also liked.

• Descriptive Statistics | Definitions, Types, Examples
• Inferential Statistics | An Easy Introduction & Examples
• Choosing the Right Statistical Test | Types & Examples

More interesting articles

• Akaike Information Criterion | When & How to Use It (Example)
• An Easy Introduction to Statistical Significance (With Examples)
• An Introduction to t Tests | Definitions, Formula and Examples
• ANOVA in R | A Complete Step-by-Step Guide with Examples
• Central Limit Theorem | Formula, Definition & Examples
• Central Tendency | Understanding the Mean, Median & Mode
• Chi-Square (Χ²) Distributions | Definition & Examples
• Chi-Square (Χ²) Table | Examples & Downloadable Table
• Chi-Square (Χ²) Tests | Types, Formula & Examples
• Chi-Square Goodness of Fit Test | Formula, Guide & Examples
• Chi-Square Test of Independence | Formula, Guide & Examples
• Coefficient of Determination (R²) | Calculation & Interpretation
• Correlation Coefficient | Types, Formulas & Examples
• Frequency Distribution | Tables, Types & Examples
• How to Calculate Standard Deviation (Guide) | Calculator & Examples
• How to Calculate Variance | Calculator, Analysis & Examples
• How to Find Degrees of Freedom | Definition & Formula
• How to Find Interquartile Range (IQR) | Calculator & Examples
• How to Find Outliers | 4 Ways with Examples & Explanation
• How to Find the Geometric Mean | Calculator & Formula
• How to Find the Mean | Definition, Examples & Calculator
• How to Find the Median | Definition, Examples & Calculator
• How to Find the Mode | Definition, Examples & Calculator
• How to Find the Range of a Data Set | Calculator & Formula
• Hypothesis Testing | A Step-by-Step Guide with Easy Examples
• Interval Data and How to Analyze It | Definitions & Examples
• Levels of Measurement | Nominal, Ordinal, Interval and Ratio
• Linear Regression in R | A Step-by-Step Guide & Examples
• Missing Data | Types, Explanation, & Imputation
• Multiple Linear Regression | A Quick Guide (Examples)
• Nominal Data | Definition, Examples, Data Collection & Analysis
• Normal Distribution | Examples, Formulas, & Uses
• Null and Alternative Hypotheses | Definitions & Examples
• One-way ANOVA | When and How to Use It (With Examples)
• Ordinal Data | Definition, Examples, Data Collection & Analysis
• Parameter vs Statistic | Definitions, Differences & Examples
• Pearson Correlation Coefficient (r) | Guide & Examples
• Poisson Distributions | Definition, Formula & Examples
• Probability Distribution | Formula, Types, & Examples
• Quartiles & Quantiles | Calculation, Definition & Interpretation
• Ratio Scales | Definition, Examples, & Data Analysis
• Simple Linear Regression | An Easy Introduction & Examples
• Skewness | Definition, Examples & Formula
• Statistical Power and Why It Matters | A Simple Introduction
• Student's t Table (Free Download) | Guide & Examples
• T-distribution: What it is and how to use it
• Test statistics | Definition, Interpretation, and Examples
• The Standard Normal Distribution | Calculator, Examples & Uses
• Two-Way ANOVA | Examples & When To Use It
• Type I & Type II Errors | Differences, Examples, Visualizations
• Understanding Confidence Intervals | Easy Examples & Formulas
• Understanding P values | Definition and Examples
• Variability | Calculating Range, IQR, Variance, Standard Deviation
• What is Effect Size and Why Does It Matter? (Examples)
• What Is Kurtosis? | Definition, Examples & Formula
• What Is Standard Error? | How to Calculate (Guide with Examples)

What is your plagiarism score?

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Statistics and probability

Unit 1: analyzing categorical data, unit 2: displaying and comparing quantitative data, unit 3: summarizing quantitative data, unit 4: modeling data distributions, unit 5: exploring bivariate numerical data, unit 6: study design, unit 7: probability, unit 8: counting, permutations, and combinations, unit 9: random variables, unit 10: sampling distributions, unit 11: confidence intervals, unit 12: significance tests (hypothesis testing), unit 13: two-sample inference for the difference between groups, unit 14: inference for categorical data (chi-square tests), unit 15: advanced regression (inference and transforming), unit 16: analysis of variance (anova).

Top 99+ Trending Statistics Research Topics for Students

Being a statistics student, finding the best statistics research topics is quite challenging. But not anymore; find the best statistics research topics now!!!

Statistics is one of the tough subjects because it consists of lots of formulas, equations and many more. Therefore the students need to spend their time to understand these concepts. And when it comes to finding the best statistics research project for their topics, statistics students are always looking for someone to help them. 

In this blog, we will share with you the most interesting and trending statistics research topics in 2023. It will not just help you to stand out in your class but also help you to explore more about the world.

If you face any problem regarding statistics, then don’t worry. You can get the best statistics assignment help from one of our experts.

As you know, it is always suggested that you should work on interesting topics. That is why we have mentioned the most interesting research topics for college students and high school students. Here in this blog post, we will share with you the list of 99+ awesome statistics research topics.

Why Do We Need to Have Good Statistics Research Topics?

Table of Contents

Having a good research topic will not just help you score good grades, but it will also allow you to finish your project quickly. Because whenever we work on something interesting, our productivity automatically boosts. Thus, you need not invest lots of time and effort, and you can achieve the best with minimal effort and time. 

What Are Some Interesting Research Topics?

If we talk about the interesting research topics in statistics, it can vary from student to student. But here are the key topics that are quite interesting for almost every student:-

• Literacy rate in a city.
• Abortion and pregnancy rate in the USA.
• Eating disorders in the citizens.
• Parent role in self-esteem and confidence of the student.
• Uses of AI in our daily life to business corporates.

Top 99+ Trending Statistics Research Topics For 2023

Here in this section, we will tell you more than 99 trending statistics research topics:

Sports Statistics Research Topics

• Statistical analysis for legs and head injuries in Football.
• Statistical analysis for shoulder and knee injuries in MotoGP.
• Deep statistical evaluation for the doping test in sports from the past decade.
• Statistical observation on the performance of athletes in the last Olympics.
• Role and effect of sports in the life of the student.

Psychology Research Topics for Statistics

• Deep statistical analysis of the effect of obesity on the student’s mental health in high school and college students.
• Statistical evolution to find out the suicide reason among students and adults.
• Statistics analysis to find out the effect of divorce on children in a country.
• Psychology affects women because of the gender gap in specific country areas.
• Statistics analysis to find out the cause of online bullying in students’ lives. 
• In Psychology, PTSD and descriptive tendencies are discussed.
• The function of researchers in statistical testing and probability.
• Acceptable significance and probability thresholds in clinical Psychology.
• The utilization of hypothesis and the role of P 0.05 for improved comprehension.
• What types of statistical data are typically rejected in psychology?
• The application of basic statistical principles and reasoning in psychological analysis.
• The role of correlation is when several psychological concepts are at risk.
• Actual case study learning and modeling are used to generate statistical reports.
• In psychology, naturalistic observation is used as a research sample.
• How should descriptive statistics be used to represent behavioral data sets?

Applied Statistics Research Topics

• Does education have a deep impact on the financial success of an individual?
• The investment in digital technology is having a meaningful return for corporations?
• The gap of financial wealth between rich and poor in the USA.
• A statistical approach to identify the effects of high-frequency trading in financial markets.
• Statistics analysis to determine the impact of the multi-agent model in financial markets. 

Personalized Medicine Statistics Research Topics

• Statistical analysis on the effect of methamphetamine on substance abusers.
• Deep research on the impact of the Corona vaccine on the Omnicrone variant. 
• Find out the best cancer treatment approach between orthodox therapies and alternative therapies.
• Statistics analysis to identify the role of genes in the child’s overall immunity.
• What factors help the patients to survive from Coronavirus .

Experimental Design Statistics Research Topics

• Generic vs private education is one of the best for the students and has better financial return.
• Psychology vs physiology: which leads the person not to quit their addictions?
• Effect of breastmilk vs packed milk on the infant child overall development
• Which causes more accidents: male alcoholics vs female alcoholics.
• What causes the student not to reveal the cyberbullying in front of their parents in most cases. 

Easy Statistics Research Topics

• Application of statistics in the world of data science
• Statistics for finance: how statistics is helping the company to grow their finance
• Advantages and disadvantages of Radar chart
• Minor marriages in south-east Asia and African countries.
• Discussion of ANOVA and correlation.
• What statistical methods are most effective for active sports?
• When measuring the correctness of college tests, a ranking statistical approach is used.
• Statistics play an important role in Data Mining operations.
• The practical application of heat estimation in engineering fields.
• In the field of speech recognition, statistical analysis is used.
• Estimating probiotics: how much time is necessary for an accurate statistical sample?
• How will the United States population grow in the next twenty years?
• The legislation and statistical reports deal with contentious issues.
• The application of empirical entropy approaches with online grammar checking.
• Transparency in statistical methodology and the reporting system of the United States Census Bureau.

Statistical Research Topics for High School

• Uses of statistics in chemometrics
• Statistics in business analytics and business intelligence
• Importance of statistics in physics.
• Deep discussion about multivariate statistics
• Uses of Statistics in machine learning

Survey Topics for Statistics

• Gather the data of the most qualified professionals in a specific area.
• Survey the time wasted by the students in watching Tvs or Netflix.
• Have a survey the fully vaccinated people in the USA 
• Gather information on the effect of a government survey on the life of citizens
• Survey to identify the English speakers in the world.

Statistics Research Paper Topics for Graduates

• Have a deep decision of Bayes theorems
• Discuss the Bayesian hierarchical models
• Analysis of the process of Japanese restaurants. 
• Deep analysis of Lévy’s continuity theorem
• Analysis of the principle of maximum entropy

AP Statistics Topics

• Discuss about the importance of econometrics
• Analyze the pros and cons of Probit Model
• Types of probability models and their uses
• Deep discussion of ortho stochastic matrix
• Find out the ways to get an adjacency matrix quickly

Good Statistics Research Topics 

• National income and the regulation of cryptocurrency.
• The benefits and drawbacks of regression analysis.
• How can estimate methods be used to correct statistical differences?
• Mathematical prediction models vs observation tactics.
• In sociology research, there is bias in quantitative data analysis.
• Inferential analytical approaches vs. descriptive statistics.
• How reliable are AI-based methods in statistical analysis?
• The internet news reporting and the fluctuations: statistics reports.
• The importance of estimate in modeled statistics and artificial sampling.

Business Statistics Topics

• Role of statistics in business in 2023
• Importance of business statistics and analytics
• What is the role of central tendency and dispersion in statistics
• Best process of sampling business data.
• Importance of statistics in big data.
• The characteristics of business data sampling: benefits and cons of software solutions.
• How may two different business tasks be tackled concurrently using linear regression analysis?
• In economic data relations, index numbers, random probability, and correctness are all important.
• The advantages of a dataset approach to statistics in programming statistics.
• Commercial statistics: how should the data be prepared for maximum accuracy?

Statistical Research Topics for College Students

• Evaluate the role of John Tukey’s contribution to statistics.
• The role of statistics to improve ADHD treatment.
• The uses and timeline of probability in statistics.
• Deep analysis of Gertrude Cox’s experimental design in statistics.
• Discuss about Florence Nightingale in statistics.
• What sorts of music do college students prefer?
• The Main Effect of Different Subjects on Student Performance.
• The Importance of Analytics in Statistics Research.
• The Influence of a Better Student in Class.
• Do extracurricular activities help in the transformation of personalities?
• Backbenchers’ Impact on Class Performance.
• Medication’s Importance in Class Performance.
• Are e-books better than traditional books?
• Choosing aspects of a subject in college

How To Write Good Statistics Research Topics?

So, the main question that arises here is how you can write good statistics research topics. The trick is understanding the methodology that is used to collect and interpret statistical data. However, if you are trying to pick any topic for your statistics project, you must think about it before going any further. 

As a result, it will teach you about the data types that will be researched because the sample will be chosen correctly. On the other hand, your basic outline for choosing the correct topics is as follows:

• Introduction of a problem
• Methodology explanation and choice. 
• Statistical research itself is in the main part (Body Part). 
• Samples deviations and variables. 
• Lastly, statistical interpretation is your last part (conclusion). 

Note:   Always include the sources from which you obtained the statistics data.

Top 3 Tips to Choose Good Statistics Research Topics

It can be quite easy for some students to pick a good statistics research topic without the help of an essay writer. But we know that it is not a common scenario for every student. That is why we will mention some of the best tips that will help you choose good statistics research topics for your next project. Either you are in a hurry or have enough time to explore. These tips will help you in every scenario.

1. Narrow down your research topic

We all start with many topics as we are not sure about our specific interests or niche. The initial step to picking up a good research topic for college or school students is to narrow down the research topic.

For this, you need to categorize the matter first. And then pick a specific category as per your interest. After that, brainstorm about the topic’s content and how you can make the points catchy, focused, directional, clear, and specific. 

2. Choose a topic that gives you curiosity

After categorizing the statistics research topics, it is time to pick one from the category. Don’t pick the most common topic because it will not help your grades and knowledge. Instead of it, please choose the best one, in which you have little information, or you are more likely to explore it.

In a statistics research paper, you always can explore something beyond your studies. By doing this, you will be more energetic to work on this project. And you will also feel glad to get them lots of information you were willing to have but didn’t get because of any reasons.

It will also make your professor happy to see your work. Ultimately it will affect your grades with a positive attitude.

3. Choose a manageable topic

Now you have decided on the topic, but you need to make sure that your research topic should be manageable. You will have limited time and resources to complete your project if you pick one of the deep statistics research topics with massive information.

Then you will struggle at the last moment and most probably not going to finish your project on time. Therefore, spend enough time exploring the topic and have a good idea about the time duration and resources you will use for the project. 

Statistics research topics are massive in numbers. Because statistics operations can be performed on anything from our psychology to our fitness. Therefore there are lots more statistics research topics to explore. But if you are not finding it challenging, then you can take the help of our statistics experts . They will help you to pick the most interesting and trending statistics research topics for your projects. 

With this help, you can also save your precious time to invest it in something else. You can also come up with a plethora of topics of your choice and we will help you to pick the best one among them. Apart from that, if you are working on a project and you are not sure whether that is the topic that excites you to work on it or not. Then we can also help you to clear all your doubts on the statistics research topic. 

Frequently Asked Questions

Q1. what are some good topics for the statistics project.

Have a look at some good topics for statistics projects:- 1. Research the average height and physics of basketball players. 2. Birth and death rate in a specific city or country. 3. Study on the obesity rate of children and adults in the USA. 4. The growth rate of China in the past few years 5. Major causes of injury in Football

Q2. What are the topics in statistics?

Statistics has lots of topics. It is hard to cover all of them in a short answer. But here are the major ones: conditional probability, variance, random variable, probability distributions, common discrete, and many more. 

Q3. What are the top 10 research topics?

Here are the top 10 research topics that you can try in 2023:

1. Plant Science 2. Mental health 3. Nutritional Immunology 4. Mood disorders 5. Aging brains 6. Infectious disease 7. Music therapy 8. Political misinformation 9. Canine Connection 10. Sustainable agriculture

Related Posts

How to Find the Best Online Statistics Homework Help

Why SPSS Homework Help Is An Important aspect for Students?

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 26 March 2024

Predicting and improving complex beer flavor through machine learning

• Michiel Schreurs   ORCID: orcid.org/0000-0002-9449-5619 1 , 2 , 3   na1 ,
• Supinya Piampongsant 1 , 2 , 3   na1 ,
• Miguel Roncoroni   ORCID: orcid.org/0000-0001-7461-1427 1 , 2 , 3   na1 ,
• Lloyd Cool   ORCID: orcid.org/0000-0001-9936-3124 1 , 2 , 3 , 4 ,
• Beatriz Herrera-Malaver   ORCID: orcid.org/0000-0002-5096-9974 1 , 2 , 3 ,
• Christophe Vanderaa   ORCID: orcid.org/0000-0001-7443-5427 4 ,
• Florian A. Theßeling 1 , 2 , 3 ,
• Łukasz Kreft   ORCID: orcid.org/0000-0001-7620-4657 5 ,
• Alexander Botzki   ORCID: orcid.org/0000-0001-6691-4233 5 ,
• Philippe Malcorps 6 ,
• Luk Daenen 6 ,
• Tom Wenseleers   ORCID: orcid.org/0000-0002-1434-861X 4 &
• Kevin J. Verstrepen   ORCID: orcid.org/0000-0002-3077-6219 1 , 2 , 3  

Nature Communications volume  15 , Article number:  2368 ( 2024 ) Cite this article

50k Accesses

850 Altmetric

Metrics details

• Chemical engineering
• Gas chromatography
• Machine learning
• Metabolomics
• Taste receptors

The perception and appreciation of food flavor depends on many interacting chemical compounds and external factors, and therefore proves challenging to understand and predict. Here, we combine extensive chemical and sensory analyses of 250 different beers to train machine learning models that allow predicting flavor and consumer appreciation. For each beer, we measure over 200 chemical properties, perform quantitative descriptive sensory analysis with a trained tasting panel and map data from over 180,000 consumer reviews to train 10 different machine learning models. The best-performing algorithm, Gradient Boosting, yields models that significantly outperform predictions based on conventional statistics and accurately predict complex food features and consumer appreciation from chemical profiles. Model dissection allows identifying specific and unexpected compounds as drivers of beer flavor and appreciation. Adding these compounds results in variants of commercial alcoholic and non-alcoholic beers with improved consumer appreciation. Together, our study reveals how big data and machine learning uncover complex links between food chemistry, flavor and consumer perception, and lays the foundation to develop novel, tailored foods with superior flavors.

Similar content being viewed by others

BitterSweet: Building machine learning models for predicting the bitter and sweet taste of small molecules

Rudraksh Tuwani, Somin Wadhwa & Ganesh Bagler

Sensory lexicon and aroma volatiles analysis of brewing malt

Xiaoxia Su, Miao Yu, … Tianyi Du

Predicting odor from molecular structure: a multi-label classification approach

Kushagra Saini & Venkatnarayan Ramanathan

Introduction

Predicting and understanding food perception and appreciation is one of the major challenges in food science. Accurate modeling of food flavor and appreciation could yield important opportunities for both producers and consumers, including quality control, product fingerprinting, counterfeit detection, spoilage detection, and the development of new products and product combinations (food pairing) 1 , 2 , 3 , 4 , 5 , 6 . Accurate models for flavor and consumer appreciation would contribute greatly to our scientific understanding of how humans perceive and appreciate flavor. Moreover, accurate predictive models would also facilitate and standardize existing food assessment methods and could supplement or replace assessments by trained and consumer tasting panels, which are variable, expensive and time-consuming 7 , 8 , 9 . Lastly, apart from providing objective, quantitative, accurate and contextual information that can help producers, models can also guide consumers in understanding their personal preferences 10 .

Despite the myriad of applications, predicting food flavor and appreciation from its chemical properties remains a largely elusive goal in sensory science, especially for complex food and beverages 11 , 12 . A key obstacle is the immense number of flavor-active chemicals underlying food flavor. Flavor compounds can vary widely in chemical structure and concentration, making them technically challenging and labor-intensive to quantify, even in the face of innovations in metabolomics, such as non-targeted metabolic fingerprinting 13 , 14 . Moreover, sensory analysis is perhaps even more complicated. Flavor perception is highly complex, resulting from hundreds of different molecules interacting at the physiochemical and sensorial level. Sensory perception is often non-linear, characterized by complex and concentration-dependent synergistic and antagonistic effects 15 , 16 , 17 , 18 , 19 , 20 , 21 that are further convoluted by the genetics, environment, culture and psychology of consumers 22 , 23 , 24 . Perceived flavor is therefore difficult to measure, with problems of sensitivity, accuracy, and reproducibility that can only be resolved by gathering sufficiently large datasets 25 . Trained tasting panels are considered the prime source of quality sensory data, but require meticulous training, are low throughput and high cost. Public databases containing consumer reviews of food products could provide a valuable alternative, especially for studying appreciation scores, which do not require formal training 25 . Public databases offer the advantage of amassing large amounts of data, increasing the statistical power to identify potential drivers of appreciation. However, public datasets suffer from biases, including a bias in the volunteers that contribute to the database, as well as confounding factors such as price, cult status and psychological conformity towards previous ratings of the product.

Classical multivariate statistics and machine learning methods have been used to predict flavor of specific compounds by, for example, linking structural properties of a compound to its potential biological activities or linking concentrations of specific compounds to sensory profiles 1 , 26 . Importantly, most previous studies focused on predicting organoleptic properties of single compounds (often based on their chemical structure) 27 , 28 , 29 , 30 , 31 , 32 , 33 , thus ignoring the fact that these compounds are present in a complex matrix in food or beverages and excluding complex interactions between compounds. Moreover, the classical statistics commonly used in sensory science 34 , 35 , 36 , 37 , 38 , 39 require a large sample size and sufficient variance amongst predictors to create accurate models. They are not fit for studying an extensive set of hundreds of interacting flavor compounds, since they are sensitive to outliers, have a high tendency to overfit and are less suited for non-linear and discontinuous relationships 40 .

In this study, we combine extensive chemical analyses and sensory data of a set of different commercial beers with machine learning approaches to develop models that predict taste, smell, mouthfeel and appreciation from compound concentrations. Beer is particularly suited to model the relationship between chemistry, flavor and appreciation. First, beer is a complex product, consisting of thousands of flavor compounds that partake in complex sensory interactions 41 , 42 , 43 . This chemical diversity arises from the raw materials (malt, yeast, hops, water and spices) and biochemical conversions during the brewing process (kilning, mashing, boiling, fermentation, maturation and aging) 44 , 45 . Second, the advent of the internet saw beer consumers embrace online review platforms, such as RateBeer (ZX Ventures, Anheuser-Busch InBev SA/NV) and BeerAdvocate (Next Glass, inc.). In this way, the beer community provides massive data sets of beer flavor and appreciation scores, creating extraordinarily large sensory databases to complement the analyses of our professional sensory panel. Specifically, we characterize over 200 chemical properties of 250 commercial beers, spread across 22 beer styles, and link these to the descriptive sensory profiling data of a 16-person in-house trained tasting panel and data acquired from over 180,000 public consumer reviews. These unique and extensive datasets enable us to train a suite of machine learning models to predict flavor and appreciation from a beer’s chemical profile. Dissection of the best-performing models allows us to pinpoint specific compounds as potential drivers of beer flavor and appreciation. Follow-up experiments confirm the importance of these compounds and ultimately allow us to significantly improve the flavor and appreciation of selected commercial beers. Together, our study represents a significant step towards understanding complex flavors and reinforces the value of machine learning to develop and refine complex foods. In this way, it represents a stepping stone for further computer-aided food engineering applications 46 .

To generate a comprehensive dataset on beer flavor, we selected 250 commercial Belgian beers across 22 different beer styles (Supplementary Fig.  S1 ). Beers with ≤ 4.2% alcohol by volume (ABV) were classified as non-alcoholic and low-alcoholic. Blonds and Tripels constitute a significant portion of the dataset (12.4% and 11.2%, respectively) reflecting their presence on the Belgian beer market and the heterogeneity of beers within these styles. By contrast, lager beers are less diverse and dominated by a handful of brands. Rare styles such as Brut or Faro make up only a small fraction of the dataset (2% and 1%, respectively) because fewer of these beers are produced and because they are dominated by distinct characteristics in terms of flavor and chemical composition.

Extensive analysis identifies relationships between chemical compounds in beer

For each beer, we measured 226 different chemical properties, including common brewing parameters such as alcohol content, iso-alpha acids, pH, sugar concentration 47 , and over 200 flavor compounds (Methods, Supplementary Table  S1 ). A large portion (37.2%) are terpenoids arising from hopping, responsible for herbal and fruity flavors 16 , 48 . A second major category are yeast metabolites, such as esters and alcohols, that result in fruity and solvent notes 48 , 49 , 50 . Other measured compounds are primarily derived from malt, or other microbes such as non- Saccharomyces yeasts and bacteria (‘wild flora’). Compounds that arise from spices or staling are labeled under ‘Others’. Five attributes (caloric value, total acids and total ester, hop aroma and sulfur compounds) are calculated from multiple individually measured compounds.

As a first step in identifying relationships between chemical properties, we determined correlations between the concentrations of the compounds (Fig.  1 , upper panel, Supplementary Data  1 and 2 , and Supplementary Fig.  S2 . For the sake of clarity, only a subset of the measured compounds is shown in Fig.  1 ). Compounds of the same origin typically show a positive correlation, while absence of correlation hints at parameters varying independently. For example, the hop aroma compounds citronellol, and alpha-terpineol show moderate correlations with each other (Spearman’s rho=0.39 and 0.57), but not with the bittering hop component iso-alpha acids (Spearman’s rho=0.16 and −0.07). This illustrates how brewers can independently modify hop aroma and bitterness by selecting hop varieties and dosage time. If hops are added early in the boiling phase, chemical conversions increase bitterness while aromas evaporate, conversely, late addition of hops preserves aroma but limits bitterness 51 . Similarly, hop-derived iso-alpha acids show a strong anti-correlation with lactic acid and acetic acid, likely reflecting growth inhibition of lactic acid and acetic acid bacteria, or the consequent use of fewer hops in sour beer styles, such as West Flanders ales and Fruit beers, that rely on these bacteria for their distinct flavors 52 . Finally, yeast-derived esters (ethyl acetate, ethyl decanoate, ethyl hexanoate, ethyl octanoate) and alcohols (ethanol, isoamyl alcohol, isobutanol, and glycerol), correlate with Spearman coefficients above 0.5, suggesting that these secondary metabolites are correlated with the yeast genetic background and/or fermentation parameters and may be difficult to influence individually, although the choice of yeast strain may offer some control 53 .

Spearman rank correlations are shown. Descriptors are grouped according to their origin (malt (blue), hops (green), yeast (red), wild flora (yellow), Others (black)), and sensory aspect (aroma, taste, palate, and overall appreciation). Please note that for the chemical compounds, for the sake of clarity, only a subset of the total number of measured compounds is shown, with an emphasis on the key compounds for each source. For more details, see the main text and Methods section. Chemical data can be found in Supplementary Data  1 , correlations between all chemical compounds are depicted in Supplementary Fig.  S2 and correlation values can be found in Supplementary Data  2 . See Supplementary Data  4 for sensory panel assessments and Supplementary Data  5 for correlation values between all sensory descriptors.

Interestingly, different beer styles show distinct patterns for some flavor compounds (Supplementary Fig.  S3 ). These observations agree with expectations for key beer styles, and serve as a control for our measurements. For instance, Stouts generally show high values for color (darker), while hoppy beers contain elevated levels of iso-alpha acids, compounds associated with bitter hop taste. Acetic and lactic acid are not prevalent in most beers, with notable exceptions such as Kriek, Lambic, Faro, West Flanders ales and Flanders Old Brown, which use acid-producing bacteria ( Lactobacillus and Pediococcus ) or unconventional yeast ( Brettanomyces ) 54 , 55 . Glycerol, ethanol and esters show similar distributions across all beer styles, reflecting their common origin as products of yeast metabolism during fermentation 45 , 53 . Finally, low/no-alcohol beers contain low concentrations of glycerol and esters. This is in line with the production process for most of the low/no-alcohol beers in our dataset, which are produced through limiting fermentation or by stripping away alcohol via evaporation or dialysis, with both methods having the unintended side-effect of reducing the amount of flavor compounds in the final beer 56 , 57 .

Besides expected associations, our data also reveals less trivial associations between beer styles and specific parameters. For example, geraniol and citronellol, two monoterpenoids responsible for citrus, floral and rose flavors and characteristic of Citra hops, are found in relatively high amounts in Christmas, Saison, and Brett/co-fermented beers, where they may originate from terpenoid-rich spices such as coriander seeds instead of hops 58 .

Tasting panel assessments reveal sensorial relationships in beer

To assess the sensory profile of each beer, a trained tasting panel evaluated each of the 250 beers for 50 sensory attributes, including different hop, malt and yeast flavors, off-flavors and spices. Panelists used a tasting sheet (Supplementary Data  3 ) to score the different attributes. Panel consistency was evaluated by repeating 12 samples across different sessions and performing ANOVA. In 95% of cases no significant difference was found across sessions ( p  > 0.05), indicating good panel consistency (Supplementary Table  S2 ).

Aroma and taste perception reported by the trained panel are often linked (Fig.  1 , bottom left panel and Supplementary Data  4 and 5 ), with high correlations between hops aroma and taste (Spearman’s rho=0.83). Bitter taste was found to correlate with hop aroma and taste in general (Spearman’s rho=0.80 and 0.69), and particularly with “grassy” noble hops (Spearman’s rho=0.75). Barnyard flavor, most often associated with sour beers, is identified together with stale hops (Spearman’s rho=0.97) that are used in these beers. Lactic and acetic acid, which often co-occur, are correlated (Spearman’s rho=0.66). Interestingly, sweetness and bitterness are anti-correlated (Spearman’s rho = −0.48), confirming the hypothesis that they mask each other 59 , 60 . Beer body is highly correlated with alcohol (Spearman’s rho = 0.79), and overall appreciation is found to correlate with multiple aspects that describe beer mouthfeel (alcohol, carbonation; Spearman’s rho= 0.32, 0.39), as well as with hop and ester aroma intensity (Spearman’s rho=0.39 and 0.35).

Similar to the chemical analyses, sensorial analyses confirmed typical features of specific beer styles (Supplementary Fig.  S4 ). For example, sour beers (Faro, Flanders Old Brown, Fruit beer, Kriek, Lambic, West Flanders ale) were rated acidic, with flavors of both acetic and lactic acid. Hoppy beers were found to be bitter and showed hop-associated aromas like citrus and tropical fruit. Malt taste is most detected among scotch, stout/porters, and strong ales, while low/no-alcohol beers, which often have a reputation for being ‘worty’ (reminiscent of unfermented, sweet malt extract) appear in the middle. Unsurprisingly, hop aromas are most strongly detected among hoppy beers. Like its chemical counterpart (Supplementary Fig.  S3 ), acidity shows a right-skewed distribution, with the most acidic beers being Krieks, Lambics, and West Flanders ales.

Tasting panel assessments of specific flavors correlate with chemical composition

We find that the concentrations of several chemical compounds strongly correlate with specific aroma or taste, as evaluated by the tasting panel (Fig.  2 , Supplementary Fig.  S5 , Supplementary Data  6 ). In some cases, these correlations confirm expectations and serve as a useful control for data quality. For example, iso-alpha acids, the bittering compounds in hops, strongly correlate with bitterness (Spearman’s rho=0.68), while ethanol and glycerol correlate with tasters’ perceptions of alcohol and body, the mouthfeel sensation of fullness (Spearman’s rho=0.82/0.62 and 0.72/0.57 respectively) and darker color from roasted malts is a good indication of malt perception (Spearman’s rho=0.54).

Heatmap colors indicate Spearman’s Rho. Axes are organized according to sensory categories (aroma, taste, mouthfeel, overall), chemical categories and chemical sources in beer (malt (blue), hops (green), yeast (red), wild flora (yellow), Others (black)). See Supplementary Data  6 for all correlation values.

Interestingly, for some relationships between chemical compounds and perceived flavor, correlations are weaker than expected. For example, the rose-smelling phenethyl acetate only weakly correlates with floral aroma. This hints at more complex relationships and interactions between compounds and suggests a need for a more complex model than simple correlations. Lastly, we uncovered unexpected correlations. For instance, the esters ethyl decanoate and ethyl octanoate appear to correlate slightly with hop perception and bitterness, possibly due to their fruity flavor. Iron is anti-correlated with hop aromas and bitterness, most likely because it is also anti-correlated with iso-alpha acids. This could be a sign of metal chelation of hop acids 61 , given that our analyses measure unbound hop acids and total iron content, or could result from the higher iron content in dark and Fruit beers, which typically have less hoppy and bitter flavors 62 .

Public consumer reviews complement expert panel data

To complement and expand the sensory data of our trained tasting panel, we collected 180,000 reviews of our 250 beers from the online consumer review platform RateBeer. This provided numerical scores for beer appearance, aroma, taste, palate, overall quality as well as the average overall score.

Public datasets are known to suffer from biases, such as price, cult status and psychological conformity towards previous ratings of a product. For example, prices correlate with appreciation scores for these online consumer reviews (rho=0.49, Supplementary Fig.  S6 ), but not for our trained tasting panel (rho=0.19). This suggests that prices affect consumer appreciation, which has been reported in wine 63 , while blind tastings are unaffected. Moreover, we observe that some beer styles, like lagers and non-alcoholic beers, generally receive lower scores, reflecting that online reviewers are mostly beer aficionados with a preference for specialty beers over lager beers. In general, we find a modest correlation between our trained panel’s overall appreciation score and the online consumer appreciation scores (Fig.  3 , rho=0.29). Apart from the aforementioned biases in the online datasets, serving temperature, sample freshness and surroundings, which are all tightly controlled during the tasting panel sessions, can vary tremendously across online consumers and can further contribute to (among others, appreciation) differences between the two categories of tasters. Importantly, in contrast to the overall appreciation scores, for many sensory aspects the results from the professional panel correlated well with results obtained from RateBeer reviews. Correlations were highest for features that are relatively easy to recognize even for untrained tasters, like bitterness, sweetness, alcohol and malt aroma (Fig.  3 and below).

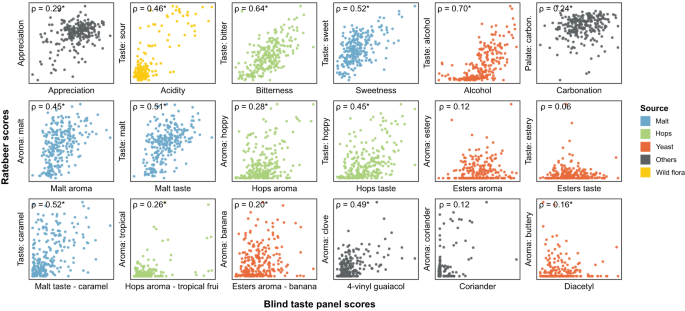
RateBeer text mining results can be found in Supplementary Data  7 . Rho values shown are Spearman correlation values, with asterisks indicating significant correlations ( p  < 0.05, two-sided). All p values were smaller than 0.001, except for Esters aroma (0.0553), Esters taste (0.3275), Esters aroma—banana (0.0019), Coriander (0.0508) and Diacetyl (0.0134).

Besides collecting consumer appreciation from these online reviews, we developed automated text analysis tools to gather additional data from review texts (Supplementary Data  7 ). Processing review texts on the RateBeer database yielded comparable results to the scores given by the trained panel for many common sensory aspects, including acidity, bitterness, sweetness, alcohol, malt, and hop tastes (Fig.  3 ). This is in line with what would be expected, since these attributes require less training for accurate assessment and are less influenced by environmental factors such as temperature, serving glass and odors in the environment. Consumer reviews also correlate well with our trained panel for 4-vinyl guaiacol, a compound associated with a very characteristic aroma. By contrast, correlations for more specific aromas like ester, coriander or diacetyl are underrepresented in the online reviews, underscoring the importance of using a trained tasting panel and standardized tasting sheets with explicit factors to be scored for evaluating specific aspects of a beer. Taken together, our results suggest that public reviews are trustworthy for some, but not all, flavor features and can complement or substitute taste panel data for these sensory aspects.

Models can predict beer sensory profiles from chemical data

The rich datasets of chemical analyses, tasting panel assessments and public reviews gathered in the first part of this study provided us with a unique opportunity to develop predictive models that link chemical data to sensorial features. Given the complexity of beer flavor, basic statistical tools such as correlations or linear regression may not always be the most suitable for making accurate predictions. Instead, we applied different machine learning models that can model both simple linear and complex interactive relationships. Specifically, we constructed a set of regression models to predict (a) trained panel scores for beer flavor and quality and (b) public reviews’ appreciation scores from beer chemical profiles. We trained and tested 10 different models (Methods), 3 linear regression-based models (simple linear regression with first-order interactions (LR), lasso regression with first-order interactions (Lasso), partial least squares regressor (PLSR)), 5 decision tree models (AdaBoost regressor (ABR), extra trees (ET), gradient boosting regressor (GBR), random forest (RF) and XGBoost regressor (XGBR)), 1 support vector regression (SVR), and 1 artificial neural network (ANN) model.

To compare the performance of our machine learning models, the dataset was randomly split into a training and test set, stratified by beer style. After a model was trained on data in the training set, its performance was evaluated on its ability to predict the test dataset obtained from multi-output models (based on the coefficient of determination, see Methods). Additionally, individual-attribute models were ranked per descriptor and the average rank was calculated, as proposed by Korneva et al. 64 . Importantly, both ways of evaluating the models’ performance agreed in general. Performance of the different models varied (Table  1 ). It should be noted that all models perform better at predicting RateBeer results than results from our trained tasting panel. One reason could be that sensory data is inherently variable, and this variability is averaged out with the large number of public reviews from RateBeer. Additionally, all tree-based models perform better at predicting taste than aroma. Linear models (LR) performed particularly poorly, with negative R 2 values, due to severe overfitting (training set R 2  = 1). Overfitting is a common issue in linear models with many parameters and limited samples, especially with interaction terms further amplifying the number of parameters. L1 regularization (Lasso) successfully overcomes this overfitting, out-competing multiple tree-based models on the RateBeer dataset. Similarly, the dimensionality reduction of PLSR avoids overfitting and improves performance, to some extent. Still, tree-based models (ABR, ET, GBR, RF and XGBR) show the best performance, out-competing the linear models (LR, Lasso, PLSR) commonly used in sensory science 65 .

GBR models showed the best overall performance in predicting sensory responses from chemical information, with R 2 values up to 0.75 depending on the predicted sensory feature (Supplementary Table  S4 ). The GBR models predict consumer appreciation (RateBeer) better than our trained panel’s appreciation (R 2 value of 0.67 compared to R 2 value of 0.09) (Supplementary Table  S3 and Supplementary Table  S4 ). ANN models showed intermediate performance, likely because neural networks typically perform best with larger datasets 66 . The SVR shows intermediate performance, mostly due to the weak predictions of specific attributes that lower the overall performance (Supplementary Table  S4 ).

Model dissection identifies specific, unexpected compounds as drivers of consumer appreciation

Next, we leveraged our models to infer important contributors to sensory perception and consumer appreciation. Consumer preference is a crucial sensory aspects, because a product that shows low consumer appreciation scores often does not succeed commercially 25 . Additionally, the requirement for a large number of representative evaluators makes consumer trials one of the more costly and time-consuming aspects of product development. Hence, a model for predicting chemical drivers of overall appreciation would be a welcome addition to the available toolbox for food development and optimization.

Since GBR models on our RateBeer dataset showed the best overall performance, we focused on these models. Specifically, we used two approaches to identify important contributors. First, rankings of the most important predictors for each sensorial trait in the GBR models were obtained based on impurity-based feature importance (mean decrease in impurity). High-ranked parameters were hypothesized to be either the true causal chemical properties underlying the trait, to correlate with the actual causal properties, or to take part in sensory interactions affecting the trait 67 (Fig.  4A ). In a second approach, we used SHAP 68 to determine which parameters contributed most to the model for making predictions of consumer appreciation (Fig.  4B ). SHAP calculates parameter contributions to model predictions on a per-sample basis, which can be aggregated into an importance score.

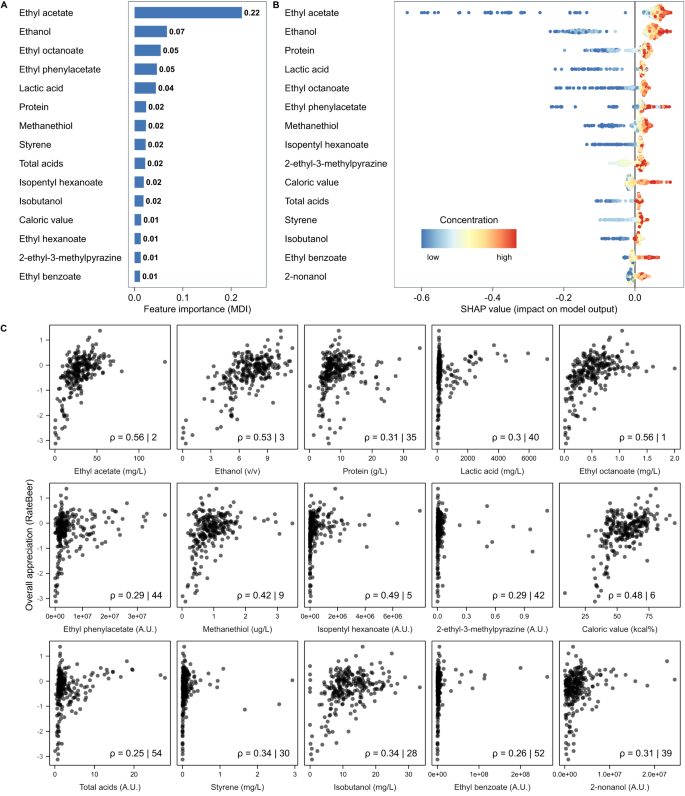
A The impurity-based feature importance (mean deviance in impurity, MDI) calculated from the Gradient Boosting Regression (GBR) model predicting RateBeer appreciation scores. The top 15 highest ranked chemical properties are shown. B SHAP summary plot for the top 15 parameters contributing to our GBR model. Each point on the graph represents a sample from our dataset. The color represents the concentration of that parameter, with bluer colors representing low values and redder colors representing higher values. Greater absolute values on the horizontal axis indicate a higher impact of the parameter on the prediction of the model. C Spearman correlations between the 15 most important chemical properties and consumer overall appreciation. Numbers indicate the Spearman Rho correlation coefficient, and the rank of this correlation compared to all other correlations. The top 15 important compounds were determined using SHAP (panel B).

Both approaches identified ethyl acetate as the most predictive parameter for beer appreciation (Fig.  4 ). Ethyl acetate is the most abundant ester in beer with a typical ‘fruity’, ‘solvent’ and ‘alcoholic’ flavor, but is often considered less important than other esters like isoamyl acetate. The second most important parameter identified by SHAP is ethanol, the most abundant beer compound after water. Apart from directly contributing to beer flavor and mouthfeel, ethanol drastically influences the physical properties of beer, dictating how easily volatile compounds escape the beer matrix to contribute to beer aroma 69 . Importantly, it should also be noted that the importance of ethanol for appreciation is likely inflated by the very low appreciation scores of non-alcoholic beers (Supplementary Fig.  S4 ). Despite not often being considered a driver of beer appreciation, protein level also ranks highly in both approaches, possibly due to its effect on mouthfeel and body 70 . Lactic acid, which contributes to the tart taste of sour beers, is the fourth most important parameter identified by SHAP, possibly due to the generally high appreciation of sour beers in our dataset.

Interestingly, some of the most important predictive parameters for our model are not well-established as beer flavors or are even commonly regarded as being negative for beer quality. For example, our models identify methanethiol and ethyl phenyl acetate, an ester commonly linked to beer staling 71 , as a key factor contributing to beer appreciation. Although there is no doubt that high concentrations of these compounds are considered unpleasant, the positive effects of modest concentrations are not yet known 72 , 73 .

To compare our approach to conventional statistics, we evaluated how well the 15 most important SHAP-derived parameters correlate with consumer appreciation (Fig.  4C ). Interestingly, only 6 of the properties derived by SHAP rank amongst the top 15 most correlated parameters. For some chemical compounds, the correlations are so low that they would have likely been considered unimportant. For example, lactic acid, the fourth most important parameter, shows a bimodal distribution for appreciation, with sour beers forming a separate cluster, that is missed entirely by the Spearman correlation. Additionally, the correlation plots reveal outliers, emphasizing the need for robust analysis tools. Together, this highlights the need for alternative models, like the Gradient Boosting model, that better grasp the complexity of (beer) flavor.

Finally, to observe the relationships between these chemical properties and their predicted targets, partial dependence plots were constructed for the six most important predictors of consumer appreciation 74 , 75 , 76 (Supplementary Fig.  S7 ). One-way partial dependence plots show how a change in concentration affects the predicted appreciation. These plots reveal an important limitation of our models: appreciation predictions remain constant at ever-increasing concentrations. This implies that once a threshold concentration is reached, further increasing the concentration does not affect appreciation. This is false, as it is well-documented that certain compounds become unpleasant at high concentrations, including ethyl acetate (‘nail polish’) 77 and methanethiol (‘sulfury’ and ‘rotten cabbage’) 78 . The inability of our models to grasp that flavor compounds have optimal levels, above which they become negative, is a consequence of working with commercial beer brands where (off-)flavors are rarely too high to negatively impact the product. The two-way partial dependence plots show how changing the concentration of two compounds influences predicted appreciation, visualizing their interactions (Supplementary Fig.  S7 ). In our case, the top 5 parameters are dominated by additive or synergistic interactions, with high concentrations for both compounds resulting in the highest predicted appreciation.

To assess the robustness of our best-performing models and model predictions, we performed 100 iterations of the GBR, RF and ET models. In general, all iterations of the models yielded similar performance (Supplementary Fig.  S8 ). Moreover, the main predictors (including the top predictors ethanol and ethyl acetate) remained virtually the same, especially for GBR and RF. For the iterations of the ET model, we did observe more variation in the top predictors, which is likely a consequence of the model’s inherent random architecture in combination with co-correlations between certain predictors. However, even in this case, several of the top predictors (ethanol and ethyl acetate) remain unchanged, although their rank in importance changes (Supplementary Fig.  S8 ).

Next, we investigated if a combination of RateBeer and trained panel data into one consolidated dataset would lead to stronger models, under the hypothesis that such a model would suffer less from bias in the datasets. A GBR model was trained to predict appreciation on the combined dataset. This model underperformed compared to the RateBeer model, both in the native case and when including a dataset identifier (R 2  = 0.67, 0.26 and 0.42 respectively). For the latter, the dataset identifier is the most important feature (Supplementary Fig.  S9 ), while most of the feature importance remains unchanged, with ethyl acetate and ethanol ranking highest, like in the original model trained only on RateBeer data. It seems that the large variation in the panel dataset introduces noise, weakening the models’ performances and reliability. In addition, it seems reasonable to assume that both datasets are fundamentally different, with the panel dataset obtained by blind tastings by a trained professional panel.

Lastly, we evaluated whether beer style identifiers would further enhance the model’s performance. A GBR model was trained with parameters that explicitly encoded the styles of the samples. This did not improve model performance (R2 = 0.66 with style information vs R2 = 0.67). The most important chemical features are consistent with the model trained without style information (eg. ethanol and ethyl acetate), and with the exception of the most preferred (strong ale) and least preferred (low/no-alcohol) styles, none of the styles were among the most important features (Supplementary Fig.  S9 , Supplementary Table  S5 and S6 ). This is likely due to a combination of style-specific chemical signatures, such as iso-alpha acids and lactic acid, that implicitly convey style information to the original models, as well as the low number of samples belonging to some styles, making it difficult for the model to learn style-specific patterns. Moreover, beer styles are not rigorously defined, with some styles overlapping in features and some beers being misattributed to a specific style, all of which leads to more noise in models that use style parameters.

Model validation

To test if our predictive models give insight into beer appreciation, we set up experiments aimed at improving existing commercial beers. We specifically selected overall appreciation as the trait to be examined because of its complexity and commercial relevance. Beer flavor comprises a complex bouquet rather than single aromas and tastes 53 . Hence, adding a single compound to the extent that a difference is noticeable may lead to an unbalanced, artificial flavor. Therefore, we evaluated the effect of combinations of compounds. Because Blond beers represent the most extensive style in our dataset, we selected a beer from this style as the starting material for these experiments (Beer 64 in Supplementary Data  1 ).

In the first set of experiments, we adjusted the concentrations of compounds that made up the most important predictors of overall appreciation (ethyl acetate, ethanol, lactic acid, ethyl phenyl acetate) together with correlated compounds (ethyl hexanoate, isoamyl acetate, glycerol), bringing them up to 95 th percentile ethanol-normalized concentrations (Methods) within the Blond group (‘Spiked’ concentration in Fig.  5A ). Compared to controls, the spiked beers were found to have significantly improved overall appreciation among trained panelists, with panelist noting increased intensity of ester flavors, sweetness, alcohol, and body fullness (Fig.  5B ). To disentangle the contribution of ethanol to these results, a second experiment was performed without the addition of ethanol. This resulted in a similar outcome, including increased perception of alcohol and overall appreciation.

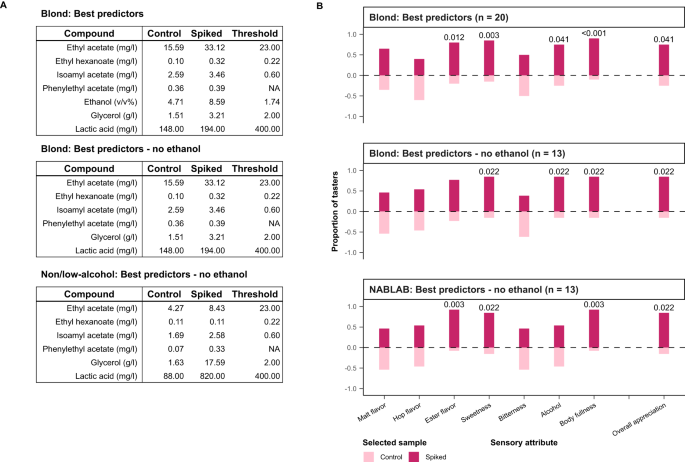
Adding the top chemical compounds, identified as best predictors of appreciation by our model, into poorly appreciated beers results in increased appreciation from our trained panel. Results of sensory tests between base beers and those spiked with compounds identified as the best predictors by the model. A Blond and Non/Low-alcohol (0.0% ABV) base beers were brought up to 95th-percentile ethanol-normalized concentrations within each style. B For each sensory attribute, tasters indicated the more intense sample and selected the sample they preferred. The numbers above the bars correspond to the p values that indicate significant changes in perceived flavor (two-sided binomial test: alpha 0.05, n  = 20 or 13).

In a last experiment, we tested whether using the model’s predictions can boost the appreciation of a non-alcoholic beer (beer 223 in Supplementary Data  1 ). Again, the addition of a mixture of predicted compounds (omitting ethanol, in this case) resulted in a significant increase in appreciation, body, ester flavor and sweetness.

Predicting flavor and consumer appreciation from chemical composition is one of the ultimate goals of sensory science. A reliable, systematic and unbiased way to link chemical profiles to flavor and food appreciation would be a significant asset to the food and beverage industry. Such tools would substantially aid in quality control and recipe development, offer an efficient and cost-effective alternative to pilot studies and consumer trials and would ultimately allow food manufacturers to produce superior, tailor-made products that better meet the demands of specific consumer groups more efficiently.

A limited set of studies have previously tried, to varying degrees of success, to predict beer flavor and beer popularity based on (a limited set of) chemical compounds and flavors 79 , 80 . Current sensitive, high-throughput technologies allow measuring an unprecedented number of chemical compounds and properties in a large set of samples, yielding a dataset that can train models that help close the gaps between chemistry and flavor, even for a complex natural product like beer. To our knowledge, no previous research gathered data at this scale (250 samples, 226 chemical parameters, 50 sensory attributes and 5 consumer scores) to disentangle and validate the chemical aspects driving beer preference using various machine-learning techniques. We find that modern machine learning models outperform conventional statistical tools, such as correlations and linear models, and can successfully predict flavor appreciation from chemical composition. This could be attributed to the natural incorporation of interactions and non-linear or discontinuous effects in machine learning models, which are not easily grasped by the linear model architecture. While linear models and partial least squares regression represent the most widespread statistical approaches in sensory science, in part because they allow interpretation 65 , 81 , 82 , modern machine learning methods allow for building better predictive models while preserving the possibility to dissect and exploit the underlying patterns. Of the 10 different models we trained, tree-based models, such as our best performing GBR, showed the best overall performance in predicting sensory responses from chemical information, outcompeting artificial neural networks. This agrees with previous reports for models trained on tabular data 83 . Our results are in line with the findings of Colantonio et al. who also identified the gradient boosting architecture as performing best at predicting appreciation and flavor (of tomatoes and blueberries, in their specific study) 26 . Importantly, besides our larger experimental scale, we were able to directly confirm our models’ predictions in vivo.

Our study confirms that flavor compound concentration does not always correlate with perception, suggesting complex interactions that are often missed by more conventional statistics and simple models. Specifically, we find that tree-based algorithms may perform best in developing models that link complex food chemistry with aroma. Furthermore, we show that massive datasets of untrained consumer reviews provide a valuable source of data, that can complement or even replace trained tasting panels, especially for appreciation and basic flavors, such as sweetness and bitterness. This holds despite biases that are known to occur in such datasets, such as price or conformity bias. Moreover, GBR models predict taste better than aroma. This is likely because taste (e.g. bitterness) often directly relates to the corresponding chemical measurements (e.g., iso-alpha acids), whereas such a link is less clear for aromas, which often result from the interplay between multiple volatile compounds. We also find that our models are best at predicting acidity and alcohol, likely because there is a direct relation between the measured chemical compounds (acids and ethanol) and the corresponding perceived sensorial attribute (acidity and alcohol), and because even untrained consumers are generally able to recognize these flavors and aromas.

The predictions of our final models, trained on review data, hold even for blind tastings with small groups of trained tasters, as demonstrated by our ability to validate specific compounds as drivers of beer flavor and appreciation. Since adding a single compound to the extent of a noticeable difference may result in an unbalanced flavor profile, we specifically tested our identified key drivers as a combination of compounds. While this approach does not allow us to validate if a particular single compound would affect flavor and/or appreciation, our experiments do show that this combination of compounds increases consumer appreciation.

It is important to stress that, while it represents an important step forward, our approach still has several major limitations. A key weakness of the GBR model architecture is that amongst co-correlating variables, the largest main effect is consistently preferred for model building. As a result, co-correlating variables often have artificially low importance scores, both for impurity and SHAP-based methods, like we observed in the comparison to the more randomized Extra Trees models. This implies that chemicals identified as key drivers of a specific sensory feature by GBR might not be the true causative compounds, but rather co-correlate with the actual causative chemical. For example, the high importance of ethyl acetate could be (partially) attributed to the total ester content, ethanol or ethyl hexanoate (rho=0.77, rho=0.72 and rho=0.68), while ethyl phenylacetate could hide the importance of prenyl isobutyrate and ethyl benzoate (rho=0.77 and rho=0.76). Expanding our GBR model to include beer style as a parameter did not yield additional power or insight. This is likely due to style-specific chemical signatures, such as iso-alpha acids and lactic acid, that implicitly convey style information to the original model, as well as the smaller sample size per style, limiting the power to uncover style-specific patterns. This can be partly attributed to the curse of dimensionality, where the high number of parameters results in the models mainly incorporating single parameter effects, rather than complex interactions such as style-dependent effects 67 . A larger number of samples may overcome some of these limitations and offer more insight into style-specific effects. On the other hand, beer style is not a rigid scientific classification, and beers within one style often differ a lot, which further complicates the analysis of style as a model factor.

Our study is limited to beers from Belgian breweries. Although these beers cover a large portion of the beer styles available globally, some beer styles and consumer patterns may be missing, while other features might be overrepresented. For example, many Belgian ales exhibit yeast-driven flavor profiles, which is reflected in the chemical drivers of appreciation discovered by this study. In future work, expanding the scope to include diverse markets and beer styles could lead to the identification of even more drivers of appreciation and better models for special niche products that were not present in our beer set.

In addition to inherent limitations of GBR models, there are also some limitations associated with studying food aroma. Even if our chemical analyses measured most of the known aroma compounds, the total number of flavor compounds in complex foods like beer is still larger than the subset we were able to measure in this study. For example, hop-derived thiols, that influence flavor at very low concentrations, are notoriously difficult to measure in a high-throughput experiment. Moreover, consumer perception remains subjective and prone to biases that are difficult to avoid. It is also important to stress that the models are still immature and that more extensive datasets will be crucial for developing more complete models in the future. Besides more samples and parameters, our dataset does not include any demographic information about the tasters. Including such data could lead to better models that grasp external factors like age and culture. Another limitation is that our set of beers consists of high-quality end-products and lacks beers that are unfit for sale, which limits the current model in accurately predicting products that are appreciated very badly. Finally, while models could be readily applied in quality control, their use in sensory science and product development is restrained by their inability to discern causal relationships. Given that the models cannot distinguish compounds that genuinely drive consumer perception from those that merely correlate, validation experiments are essential to identify true causative compounds.

Despite the inherent limitations, dissection of our models enabled us to pinpoint specific molecules as potential drivers of beer aroma and consumer appreciation, including compounds that were unexpected and would not have been identified using standard approaches. Important drivers of beer appreciation uncovered by our models include protein levels, ethyl acetate, ethyl phenyl acetate and lactic acid. Currently, many brewers already use lactic acid to acidify their brewing water and ensure optimal pH for enzymatic activity during the mashing process. Our results suggest that adding lactic acid can also improve beer appreciation, although its individual effect remains to be tested. Interestingly, ethanol appears to be unnecessary to improve beer appreciation, both for blond beer and alcohol-free beer. Given the growing consumer interest in alcohol-free beer, with a predicted annual market growth of >7% 84 , it is relevant for brewers to know what compounds can further increase consumer appreciation of these beers. Hence, our model may readily provide avenues to further improve the flavor and consumer appreciation of both alcoholic and non-alcoholic beers, which is generally considered one of the key challenges for future beer production.

Whereas we see a direct implementation of our results for the development of superior alcohol-free beverages and other food products, our study can also serve as a stepping stone for the development of novel alcohol-containing beverages. We want to echo the growing body of scientific evidence for the negative effects of alcohol consumption, both on the individual level by the mutagenic, teratogenic and carcinogenic effects of ethanol 85 , 86 , as well as the burden on society caused by alcohol abuse and addiction. We encourage the use of our results for the production of healthier, tastier products, including novel and improved beverages with lower alcohol contents. Furthermore, we strongly discourage the use of these technologies to improve the appreciation or addictive properties of harmful substances.

The present work demonstrates that despite some important remaining hurdles, combining the latest developments in chemical analyses, sensory analysis and modern machine learning methods offers exciting avenues for food chemistry and engineering. Soon, these tools may provide solutions in quality control and recipe development, as well as new approaches to sensory science and flavor research.

Beer selection

250 commercial Belgian beers were selected to cover the broad diversity of beer styles and corresponding diversity in chemical composition and aroma. See Supplementary Fig.  S1 .

Chemical dataset

Sample preparation.

Beers within their expiration date were purchased from commercial retailers. Samples were prepared in biological duplicates at room temperature, unless explicitly stated otherwise. Bottle pressure was measured with a manual pressure device (Steinfurth Mess-Systeme GmbH) and used to calculate CO 2 concentration. The beer was poured through two filter papers (Macherey-Nagel, 500713032 MN 713 ¼) to remove carbon dioxide and prevent spontaneous foaming. Samples were then prepared for measurements by targeted Headspace-Gas Chromatography-Flame Ionization Detector/Flame Photometric Detector (HS-GC-FID/FPD), Headspace-Solid Phase Microextraction-Gas Chromatography-Mass Spectrometry (HS-SPME-GC-MS), colorimetric analysis, enzymatic analysis, Near-Infrared (NIR) analysis, as described in the sections below. The mean values of biological duplicates are reported for each compound.

HS-GC-FID/FPD

HS-GC-FID/FPD (Shimadzu GC 2010 Plus) was used to measure higher alcohols, acetaldehyde, esters, 4-vinyl guaicol, and sulfur compounds. Each measurement comprised 5 ml of sample pipetted into a 20 ml glass vial containing 1.75 g NaCl (VWR, 27810.295). 100 µl of 2-heptanol (Sigma-Aldrich, H3003) (internal standard) solution in ethanol (Fisher Chemical, E/0650DF/C17) was added for a final concentration of 2.44 mg/L. Samples were flushed with nitrogen for 10 s, sealed with a silicone septum, stored at −80 °C and analyzed in batches of 20.

The GC was equipped with a DB-WAXetr column (length, 30 m; internal diameter, 0.32 mm; layer thickness, 0.50 µm; Agilent Technologies, Santa Clara, CA, USA) to the FID and an HP-5 column (length, 30 m; internal diameter, 0.25 mm; layer thickness, 0.25 µm; Agilent Technologies, Santa Clara, CA, USA) to the FPD. N 2 was used as the carrier gas. Samples were incubated for 20 min at 70 °C in the headspace autosampler (Flow rate, 35 cm/s; Injection volume, 1000 µL; Injection mode, split; Combi PAL autosampler, CTC analytics, Switzerland). The injector, FID and FPD temperatures were kept at 250 °C. The GC oven temperature was first held at 50 °C for 5 min and then allowed to rise to 80 °C at a rate of 5 °C/min, followed by a second ramp of 4 °C/min until 200 °C kept for 3 min and a final ramp of (4 °C/min) until 230 °C for 1 min. Results were analyzed with the GCSolution software version 2.4 (Shimadzu, Kyoto, Japan). The GC was calibrated with a 5% EtOH solution (VWR International) containing the volatiles under study (Supplementary Table  S7 ).

HS-SPME-GC-MS

HS-SPME-GC-MS (Shimadzu GCMS-QP-2010 Ultra) was used to measure additional volatile compounds, mainly comprising terpenoids and esters. Samples were analyzed by HS-SPME using a triphase DVB/Carboxen/PDMS 50/30 μm SPME fiber (Supelco Co., Bellefonte, PA, USA) followed by gas chromatography (Thermo Fisher Scientific Trace 1300 series, USA) coupled to a mass spectrometer (Thermo Fisher Scientific ISQ series MS) equipped with a TriPlus RSH autosampler. 5 ml of degassed beer sample was placed in 20 ml vials containing 1.75 g NaCl (VWR, 27810.295). 5 µl internal standard mix was added, containing 2-heptanol (1 g/L) (Sigma-Aldrich, H3003), 4-fluorobenzaldehyde (1 g/L) (Sigma-Aldrich, 128376), 2,3-hexanedione (1 g/L) (Sigma-Aldrich, 144169) and guaiacol (1 g/L) (Sigma-Aldrich, W253200) in ethanol (Fisher Chemical, E/0650DF/C17). Each sample was incubated at 60 °C in the autosampler oven with constant agitation. After 5 min equilibration, the SPME fiber was exposed to the sample headspace for 30 min. The compounds trapped on the fiber were thermally desorbed in the injection port of the chromatograph by heating the fiber for 15 min at 270 °C.

The GC-MS was equipped with a low polarity RXi-5Sil MS column (length, 20 m; internal diameter, 0.18 mm; layer thickness, 0.18 µm; Restek, Bellefonte, PA, USA). Injection was performed in splitless mode at 320 °C, a split flow of 9 ml/min, a purge flow of 5 ml/min and an open valve time of 3 min. To obtain a pulsed injection, a programmed gas flow was used whereby the helium gas flow was set at 2.7 mL/min for 0.1 min, followed by a decrease in flow of 20 ml/min to the normal 0.9 mL/min. The temperature was first held at 30 °C for 3 min and then allowed to rise to 80 °C at a rate of 7 °C/min, followed by a second ramp of 2 °C/min till 125 °C and a final ramp of 8 °C/min with a final temperature of 270 °C.

Mass acquisition range was 33 to 550 amu at a scan rate of 5 scans/s. Electron impact ionization energy was 70 eV. The interface and ion source were kept at 275 °C and 250 °C, respectively. A mix of linear n-alkanes (from C7 to C40, Supelco Co.) was injected into the GC-MS under identical conditions to serve as external retention index markers. Identification and quantification of the compounds were performed using an in-house developed R script as described in Goelen et al. and Reher et al. 87 , 88 (for package information, see Supplementary Table  S8 ). Briefly, chromatograms were analyzed using AMDIS (v2.71) 89 to separate overlapping peaks and obtain pure compound spectra. The NIST MS Search software (v2.0 g) in combination with the NIST2017, FFNSC3 and Adams4 libraries were used to manually identify the empirical spectra, taking into account the expected retention time. After background subtraction and correcting for retention time shifts between samples run on different days based on alkane ladders, compound elution profiles were extracted and integrated using a file with 284 target compounds of interest, which were either recovered in our identified AMDIS list of spectra or were known to occur in beer. Compound elution profiles were estimated for every peak in every chromatogram over a time-restricted window using weighted non-negative least square analysis after which peak areas were integrated 87 , 88 . Batch effect correction was performed by normalizing against the most stable internal standard compound, 4-fluorobenzaldehyde. Out of all 284 target compounds that were analyzed, 167 were visually judged to have reliable elution profiles and were used for final analysis.

Discrete photometric and enzymatic analysis

Discrete photometric and enzymatic analysis (Thermo Scientific TM Gallery TM Plus Beermaster Discrete Analyzer) was used to measure acetic acid, ammonia, beta-glucan, iso-alpha acids, color, sugars, glycerol, iron, pH, protein, and sulfite. 2 ml of sample volume was used for the analyses. Information regarding the reagents and standard solutions used for analyses and calibrations is included in Supplementary Table  S7 and Supplementary Table  S9 .

NIR analyses

NIR analysis (Anton Paar Alcolyzer Beer ME System) was used to measure ethanol. Measurements comprised 50 ml of sample, and a 10% EtOH solution was used for calibration.

Correlation calculations

Pairwise Spearman Rank correlations were calculated between all chemical properties.

Sensory dataset

Trained panel.

Our trained tasting panel consisted of volunteers who gave prior verbal informed consent. All compounds used for the validation experiment were of food-grade quality. The tasting sessions were approved by the Social and Societal Ethics Committee of the KU Leuven (G-2022-5677-R2(MAR)). All online reviewers agreed to the Terms and Conditions of the RateBeer website.

Sensory analysis was performed according to the American Society of Brewing Chemists (ASBC) Sensory Analysis Methods 90 . 30 volunteers were screened through a series of triangle tests. The sixteen most sensitive and consistent tasters were retained as taste panel members. The resulting panel was diverse in age [22–42, mean: 29], sex [56% male] and nationality [7 different countries]. The panel developed a consensus vocabulary to describe beer aroma, taste and mouthfeel. Panelists were trained to identify and score 50 different attributes, using a 7-point scale to rate attributes’ intensity. The scoring sheet is included as Supplementary Data  3 . Sensory assessments took place between 10–12 a.m. The beers were served in black-colored glasses. Per session, between 5 and 12 beers of the same style were tasted at 12 °C to 16 °C. Two reference beers were added to each set and indicated as ‘Reference 1 & 2’, allowing panel members to calibrate their ratings. Not all panelists were present at every tasting. Scores were scaled by standard deviation and mean-centered per taster. Values are represented as z-scores and clustered by Euclidean distance. Pairwise Spearman correlations were calculated between taste and aroma sensory attributes. Panel consistency was evaluated by repeating samples on different sessions and performing ANOVA to identify differences, using the ‘stats’ package (v4.2.2) in R (for package information, see Supplementary Table  S8 ).

Online reviews from a public database

The ‘scrapy’ package in Python (v3.6) (for package information, see Supplementary Table  S8 ). was used to collect 232,288 online reviews (mean=922, min=6, max=5343) from RateBeer, an online beer review database. Each review entry comprised 5 numerical scores (appearance, aroma, taste, palate and overall quality) and an optional review text. The total number of reviews per reviewer was collected separately. Numerical scores were scaled and centered per rater, and mean scores were calculated per beer.

For the review texts, the language was estimated using the packages ‘langdetect’ and ‘langid’ in Python. Reviews that were classified as English by both packages were kept. Reviewers with fewer than 100 entries overall were discarded. 181,025 reviews from >6000 reviewers from >40 countries remained. Text processing was done using the ‘nltk’ package in Python. Texts were corrected for slang and misspellings; proper nouns and rare words that are relevant to the beer context were specified and kept as-is (‘Chimay’,’Lambic’, etc.). A dictionary of semantically similar sensorial terms, for example ‘floral’ and ‘flower’, was created and collapsed together into one term. Words were stemmed and lemmatized to avoid identifying words such as ‘acid’ and ‘acidity’ as separate terms. Numbers and punctuation were removed.

Sentences from up to 50 randomly chosen reviews per beer were manually categorized according to the aspect of beer they describe (appearance, aroma, taste, palate, overall quality—not to be confused with the 5 numerical scores described above) or flagged as irrelevant if they contained no useful information. If a beer contained fewer than 50 reviews, all reviews were manually classified. This labeled data set was used to train a model that classified the rest of the sentences for all beers 91 . Sentences describing taste and aroma were extracted, and term frequency–inverse document frequency (TFIDF) was implemented to calculate enrichment scores for sensorial words per beer.

The sex of the tasting subject was not considered when building our sensory database. Instead, results from different panelists were averaged, both for our trained panel (56% male, 44% female) and the RateBeer reviews (70% male, 30% female for RateBeer as a whole).

Beer price collection and processing

Beer prices were collected from the following stores: Colruyt, Delhaize, Total Wine, BeerHawk, The Belgian Beer Shop, The Belgian Shop, and Beer of Belgium. Where applicable, prices were converted to Euros and normalized per liter. Spearman correlations were calculated between these prices and mean overall appreciation scores from RateBeer and the taste panel, respectively.

Pairwise Spearman Rank correlations were calculated between all sensory properties.

Machine learning models

Predictive modeling of sensory profiles from chemical data.

Regression models were constructed to predict (a) trained panel scores for beer flavors and quality from beer chemical profiles and (b) public reviews’ appreciation scores from beer chemical profiles. Z-scores were used to represent sensory attributes in both data sets. Chemical properties with log-normal distributions (Shapiro-Wilk test, p  <  0.05 ) were log-transformed. Missing chemical measurements (0.1% of all data) were replaced with mean values per attribute. Observations from 250 beers were randomly separated into a training set (70%, 175 beers) and a test set (30%, 75 beers), stratified per beer style. Chemical measurements (p = 231) were normalized based on the training set average and standard deviation. In total, three linear regression-based models: linear regression with first-order interaction terms (LR), lasso regression with first-order interaction terms (Lasso) and partial least squares regression (PLSR); five decision tree models, Adaboost regressor (ABR), Extra Trees (ET), Gradient Boosting regressor (GBR), Random Forest (RF) and XGBoost regressor (XGBR); one support vector machine model (SVR) and one artificial neural network model (ANN) were trained. The models were implemented using the ‘scikit-learn’ package (v1.2.2) and ‘xgboost’ package (v1.7.3) in Python (v3.9.16). Models were trained, and hyperparameters optimized, using five-fold cross-validated grid search with the coefficient of determination (R 2 ) as the evaluation metric. The ANN (scikit-learn’s MLPRegressor) was optimized using Bayesian Tree-Structured Parzen Estimator optimization with the ‘Optuna’ Python package (v3.2.0). Individual models were trained per attribute, and a multi-output model was trained on all attributes simultaneously.

Model dissection

GBR was found to outperform other methods, resulting in models with the highest average R 2 values in both trained panel and public review data sets. Impurity-based rankings of the most important predictors for each predicted sensorial trait were obtained using the ‘scikit-learn’ package. To observe the relationships between these chemical properties and their predicted targets, partial dependence plots (PDP) were constructed for the six most important predictors of consumer appreciation 74 , 75 .

The ‘SHAP’ package in Python (v0.41.0) was implemented to provide an alternative ranking of predictor importance and to visualize the predictors’ effects as a function of their concentration 68 .

Validation of causal chemical properties

To validate the effects of the most important model features on predicted sensory attributes, beers were spiked with the chemical compounds identified by the models and descriptive sensory analyses were carried out according to the American Society of Brewing Chemists (ASBC) protocol 90 .

Compound spiking was done 30 min before tasting. Compounds were spiked into fresh beer bottles, that were immediately resealed and inverted three times. Fresh bottles of beer were opened for the same duration, resealed, and inverted thrice, to serve as controls. Pairs of spiked samples and controls were served simultaneously, chilled and in dark glasses as outlined in the Trained panel section above. Tasters were instructed to select the glass with the higher flavor intensity for each attribute (directional difference test 92 ) and to select the glass they prefer.

The final concentration after spiking was equal to the within-style average, after normalizing by ethanol concentration. This was done to ensure balanced flavor profiles in the final spiked beer. The same methods were applied to improve a non-alcoholic beer. Compounds were the following: ethyl acetate (Merck KGaA, W241415), ethyl hexanoate (Merck KGaA, W243906), isoamyl acetate (Merck KGaA, W205508), phenethyl acetate (Merck KGaA, W285706), ethanol (96%, Colruyt), glycerol (Merck KGaA, W252506), lactic acid (Merck KGaA, 261106).

Significant differences in preference or perceived intensity were determined by performing the two-sided binomial test on each attribute.

Reporting summary

Further information on research design is available in the  Nature Portfolio Reporting Summary linked to this article.

Data availability

The data that support the findings of this work are available in the Supplementary Data files and have been deposited to Zenodo under accession code 10653704 93 . The RateBeer scores data are under restricted access, they are not publicly available as they are property of RateBeer (ZX Ventures, USA). Access can be obtained from the authors upon reasonable request and with permission of RateBeer (ZX Ventures, USA).  Source data are provided with this paper.

Code availability

The code for training the machine learning models, analyzing the models, and generating the figures has been deposited to Zenodo under accession code 10653704 93 .

Tieman, D. et al. A chemical genetic roadmap to improved tomato flavor. Science 355 , 391–394 (2017).

Article   ADS   CAS   PubMed   Google Scholar  

Plutowska, B. & Wardencki, W. Application of gas chromatography–olfactometry (GC–O) in analysis and quality assessment of alcoholic beverages – A review. Food Chem. 107 , 449–463 (2008).

Article   CAS   Google Scholar  

Legin, A., Rudnitskaya, A., Seleznev, B. & Vlasov, Y. Electronic tongue for quality assessment of ethanol, vodka and eau-de-vie. Anal. Chim. Acta 534 , 129–135 (2005).

Loutfi, A., Coradeschi, S., Mani, G. K., Shankar, P. & Rayappan, J. B. B. Electronic noses for food quality: A review. J. Food Eng. 144 , 103–111 (2015).

Ahn, Y.-Y., Ahnert, S. E., Bagrow, J. P. & Barabási, A.-L. Flavor network and the principles of food pairing. Sci. Rep. 1 , 196 (2011).

Article   CAS   PubMed   PubMed Central   Google Scholar  

Bartoshuk, L. M. & Klee, H. J. Better fruits and vegetables through sensory analysis. Curr. Biol. 23 , R374–R378 (2013).

Article   CAS   PubMed   Google Scholar  

Piggott, J. R. Design questions in sensory and consumer science. Food Qual. Prefer. 3293 , 217–220 (1995).

Article   Google Scholar  

Kermit, M. & Lengard, V. Assessing the performance of a sensory panel-panellist monitoring and tracking. J. Chemom. 19 , 154–161 (2005).

Cook, D. J., Hollowood, T. A., Linforth, R. S. T. & Taylor, A. J. Correlating instrumental measurements of texture and flavour release with human perception. Int. J. Food Sci. Technol. 40 , 631–641 (2005).

Chinchanachokchai, S., Thontirawong, P. & Chinchanachokchai, P. A tale of two recommender systems: The moderating role of consumer expertise on artificial intelligence based product recommendations. J. Retail. Consum. Serv. 61 , 1–12 (2021).

Ross, C. F. Sensory science at the human-machine interface. Trends Food Sci. Technol. 20 , 63–72 (2009).

Chambers, E. IV & Koppel, K. Associations of volatile compounds with sensory aroma and flavor: The complex nature of flavor. Molecules 18 , 4887–4905 (2013).

Pinu, F. R. Metabolomics—The new frontier in food safety and quality research. Food Res. Int. 72 , 80–81 (2015).

Danezis, G. P., Tsagkaris, A. S., Brusic, V. & Georgiou, C. A. Food authentication: state of the art and prospects. Curr. Opin. Food Sci. 10 , 22–31 (2016).

Shepherd, G. M. Smell images and the flavour system in the human brain. Nature 444 , 316–321 (2006).

Meilgaard, M. C. Prediction of flavor differences between beers from their chemical composition. J. Agric. Food Chem. 30 , 1009–1017 (1982).

Xu, L. et al. Widespread receptor-driven modulation in peripheral olfactory coding. Science 368 , eaaz5390 (2020).

Kupferschmidt, K. Following the flavor. Science 340 , 808–809 (2013).

Billesbølle, C. B. et al. Structural basis of odorant recognition by a human odorant receptor. Nature 615 , 742–749 (2023).

Article   ADS   PubMed   PubMed Central   Google Scholar  

Smith, B. Perspective: Complexities of flavour. Nature 486 , S6–S6 (2012).

Pfister, P. et al. Odorant receptor inhibition is fundamental to odor encoding. Curr. Biol. 30 , 2574–2587 (2020).

Moskowitz, H. W., Kumaraiah, V., Sharma, K. N., Jacobs, H. L. & Sharma, S. D. Cross-cultural differences in simple taste preferences. Science 190 , 1217–1218 (1975).

Eriksson, N. et al. A genetic variant near olfactory receptor genes influences cilantro preference. Flavour 1 , 22 (2012).

Ferdenzi, C. et al. Variability of affective responses to odors: Culture, gender, and olfactory knowledge. Chem. Senses 38 , 175–186 (2013).

Article   PubMed   Google Scholar  

Lawless, H. T. & Heymann, H. Sensory evaluation of food: Principles and practices. (Springer, New York, NY). https://doi.org/10.1007/978-1-4419-6488-5 (2010).

Colantonio, V. et al. Metabolomic selection for enhanced fruit flavor. Proc. Natl. Acad. Sci. 119 , e2115865119 (2022).

Fritz, F., Preissner, R. & Banerjee, P. VirtualTaste: a web server for the prediction of organoleptic properties of chemical compounds. Nucleic Acids Res 49 , W679–W684 (2021).

Tuwani, R., Wadhwa, S. & Bagler, G. BitterSweet: Building machine learning models for predicting the bitter and sweet taste of small molecules. Sci. Rep. 9 , 1–13 (2019).

Dagan-Wiener, A. et al. Bitter or not? BitterPredict, a tool for predicting taste from chemical structure. Sci. Rep. 7 , 1–13 (2017).

Pallante, L. et al. Toward a general and interpretable umami taste predictor using a multi-objective machine learning approach. Sci. Rep. 12 , 1–11 (2022).

Malavolta, M. et al. A survey on computational taste predictors. Eur. Food Res. Technol. 248 , 2215–2235 (2022).

Lee, B. K. et al. A principal odor map unifies diverse tasks in olfactory perception. Science 381 , 999–1006 (2023).

Mayhew, E. J. et al. Transport features predict if a molecule is odorous. Proc. Natl. Acad. Sci. 119 , e2116576119 (2022).

Niu, Y. et al. Sensory evaluation of the synergism among ester odorants in light aroma-type liquor by odor threshold, aroma intensity and flash GC electronic nose. Food Res. Int. 113 , 102–114 (2018).

Yu, P., Low, M. Y. & Zhou, W. Design of experiments and regression modelling in food flavour and sensory analysis: A review. Trends Food Sci. Technol. 71 , 202–215 (2018).

Oladokun, O. et al. The impact of hop bitter acid and polyphenol profiles on the perceived bitterness of beer. Food Chem. 205 , 212–220 (2016).

Linforth, R., Cabannes, M., Hewson, L., Yang, N. & Taylor, A. Effect of fat content on flavor delivery during consumption: An in vivo model. J. Agric. Food Chem. 58 , 6905–6911 (2010).

Guo, S., Na Jom, K. & Ge, Y. Influence of roasting condition on flavor profile of sunflower seeds: A flavoromics approach. Sci. Rep. 9 , 11295 (2019).

Ren, Q. et al. The changes of microbial community and flavor compound in the fermentation process of Chinese rice wine using Fagopyrum tataricum grain as feedstock. Sci. Rep. 9 , 3365 (2019).

Hastie, T., Friedman, J. & Tibshirani, R. The Elements of Statistical Learning. (Springer, New York, NY). https://doi.org/10.1007/978-0-387-21606-5 (2001).

Dietz, C., Cook, D., Huismann, M., Wilson, C. & Ford, R. The multisensory perception of hop essential oil: a review. J. Inst. Brew. 126 , 320–342 (2020).

CAS   Google Scholar  

Roncoroni, Miguel & Verstrepen, Kevin Joan. Belgian Beer: Tested and Tasted. (Lannoo, 2018).

Meilgaard, M. Flavor chemistry of beer: Part II: Flavor and threshold of 239 aroma volatiles. in (1975).

Bokulich, N. A. & Bamforth, C. W. The microbiology of malting and brewing. Microbiol. Mol. Biol. Rev. MMBR 77 , 157–172 (2013).

Dzialo, M. C., Park, R., Steensels, J., Lievens, B. & Verstrepen, K. J. Physiology, ecology and industrial applications of aroma formation in yeast. FEMS Microbiol. Rev. 41 , S95–S128 (2017).

Article   PubMed   PubMed Central   Google Scholar  

Datta, A. et al. Computer-aided food engineering. Nat. Food 3 , 894–904 (2022).

American Society of Brewing Chemists. Beer Methods. (American Society of Brewing Chemists, St. Paul, MN, U.S.A.).

Olaniran, A. O., Hiralal, L., Mokoena, M. P. & Pillay, B. Flavour-active volatile compounds in beer: production, regulation and control. J. Inst. Brew. 123 , 13–23 (2017).

Verstrepen, K. J. et al. Flavor-active esters: Adding fruitiness to beer. J. Biosci. Bioeng. 96 , 110–118 (2003).

Meilgaard, M. C. Flavour chemistry of beer. part I: flavour interaction between principal volatiles. Master Brew. Assoc. Am. Tech. Q 12 , 107–117 (1975).

Briggs, D. E., Boulton, C. A., Brookes, P. A. & Stevens, R. Brewing 227–254. (Woodhead Publishing). https://doi.org/10.1533/9781855739062.227 (2004).

Bossaert, S., Crauwels, S., De Rouck, G. & Lievens, B. The power of sour - A review: Old traditions, new opportunities. BrewingScience 72 , 78–88 (2019).

Google Scholar  

Verstrepen, K. J. et al. Flavor active esters: Adding fruitiness to beer. J. Biosci. Bioeng. 96 , 110–118 (2003).

Snauwaert, I. et al. Microbial diversity and metabolite composition of Belgian red-brown acidic ales. Int. J. Food Microbiol. 221 , 1–11 (2016).

Spitaels, F. et al. The microbial diversity of traditional spontaneously fermented lambic beer. PLoS ONE 9 , e95384 (2014).

Blanco, C. A., Andrés-Iglesias, C. & Montero, O. Low-alcohol Beers: Flavor Compounds, Defects, and Improvement Strategies. Crit. Rev. Food Sci. Nutr. 56 , 1379–1388 (2016).

Jackowski, M. & Trusek, A. Non-Alcohol. beer Prod. – Overv. 20 , 32–38 (2018).

Takoi, K. et al. The contribution of geraniol metabolism to the citrus flavour of beer: Synergy of geraniol and β-citronellol under coexistence with excess linalool. J. Inst. Brew. 116 , 251–260 (2010).

Kroeze, J. H. & Bartoshuk, L. M. Bitterness suppression as revealed by split-tongue taste stimulation in humans. Physiol. Behav. 35 , 779–783 (1985).

Mennella, J. A. et al. A spoonful of sugar helps the medicine go down”: Bitter masking bysucrose among children and adults. Chem. Senses 40 , 17–25 (2015).

Wietstock, P., Kunz, T., Perreira, F. & Methner, F.-J. Metal chelation behavior of hop acids in buffered model systems. BrewingScience 69 , 56–63 (2016).

Sancho, D., Blanco, C. A., Caballero, I. & Pascual, A. Free iron in pale, dark and alcohol-free commercial lager beers. J. Sci. Food Agric. 91 , 1142–1147 (2011).

Rodrigues, H. & Parr, W. V. Contribution of cross-cultural studies to understanding wine appreciation: A review. Food Res. Int. 115 , 251–258 (2019).

Korneva, E. & Blockeel, H. Towards better evaluation of multi-target regression models. in ECML PKDD 2020 Workshops (eds. Koprinska, I. et al.) 353–362 (Springer International Publishing, Cham, 2020). https://doi.org/10.1007/978-3-030-65965-3_23 .

Gastón Ares. Mathematical and Statistical Methods in Food Science and Technology. (Wiley, 2013).

Grinsztajn, L., Oyallon, E. & Varoquaux, G. Why do tree-based models still outperform deep learning on tabular data? Preprint at http://arxiv.org/abs/2207.08815 (2022).

Gries, S. T. Statistics for Linguistics with R: A Practical Introduction. in Statistics for Linguistics with R (De Gruyter Mouton, 2021). https://doi.org/10.1515/9783110718256 .

Lundberg, S. M. et al. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2 , 56–67 (2020).

Ickes, C. M. & Cadwallader, K. R. Effects of ethanol on flavor perception in alcoholic beverages. Chemosens. Percept. 10 , 119–134 (2017).

Kato, M. et al. Influence of high molecular weight polypeptides on the mouthfeel of commercial beer. J. Inst. Brew. 127 , 27–40 (2021).

Wauters, R. et al. Novel Saccharomyces cerevisiae variants slow down the accumulation of staling aldehydes and improve beer shelf-life. Food Chem. 398 , 1–11 (2023).

Li, H., Jia, S. & Zhang, W. Rapid determination of low-level sulfur compounds in beer by headspace gas chromatography with a pulsed flame photometric detector. J. Am. Soc. Brew. Chem. 66 , 188–191 (2008).

Dercksen, A., Laurens, J., Torline, P., Axcell, B. C. & Rohwer, E. Quantitative analysis of volatile sulfur compounds in beer using a membrane extraction interface. J. Am. Soc. Brew. Chem. 54 , 228–233 (1996).

Molnar, C. Interpretable Machine Learning: A Guide for Making Black-Box Models Interpretable. (2020).

Zhao, Q. & Hastie, T. Causal interpretations of black-box models. J. Bus. Econ. Stat. Publ. Am. Stat. Assoc. 39 , 272–281 (2019).

Article   MathSciNet   Google Scholar  

Hastie, T., Tibshirani, R. & Friedman, J. The Elements of Statistical Learning. (Springer, 2019).

Labrado, D. et al. Identification by NMR of key compounds present in beer distillates and residual phases after dealcoholization by vacuum distillation. J. Sci. Food Agric. 100 , 3971–3978 (2020).

Lusk, L. T., Kay, S. B., Porubcan, A. & Ryder, D. S. Key olfactory cues for beer oxidation. J. Am. Soc. Brew. Chem. 70 , 257–261 (2012).

Gonzalez Viejo, C., Torrico, D. D., Dunshea, F. R. & Fuentes, S. Development of artificial neural network models to assess beer acceptability based on sensory properties using a robotic pourer: A comparative model approach to achieve an artificial intelligence system. Beverages 5 , 33 (2019).

Gonzalez Viejo, C., Fuentes, S., Torrico, D. D., Godbole, A. & Dunshea, F. R. Chemical characterization of aromas in beer and their effect on consumers liking. Food Chem. 293 , 479–485 (2019).

Gilbert, J. L. et al. Identifying breeding priorities for blueberry flavor using biochemical, sensory, and genotype by environment analyses. PLOS ONE 10 , 1–21 (2015).

Goulet, C. et al. Role of an esterase in flavor volatile variation within the tomato clade. Proc. Natl. Acad. Sci. 109 , 19009–19014 (2012).

Article   ADS   CAS   PubMed   PubMed Central   Google Scholar  

Borisov, V. et al. Deep Neural Networks and Tabular Data: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 1–21 https://doi.org/10.1109/TNNLS.2022.3229161 (2022).

Statista. Statista Consumer Market Outlook: Beer - Worldwide.

Seitz, H. K. & Stickel, F. Molecular mechanisms of alcoholmediated carcinogenesis. Nat. Rev. Cancer 7 , 599–612 (2007).

Voordeckers, K. et al. Ethanol exposure increases mutation rate through error-prone polymerases. Nat. Commun. 11 , 3664 (2020).

Goelen, T. et al. Bacterial phylogeny predicts volatile organic compound composition and olfactory response of an aphid parasitoid. Oikos 129 , 1415–1428 (2020).

Article   ADS   Google Scholar  

Reher, T. et al. Evaluation of hop (Humulus lupulus) as a repellent for the management of Drosophila suzukii. Crop Prot. 124 , 104839 (2019).

Stein, S. E. An integrated method for spectrum extraction and compound identification from gas chromatography/mass spectrometry data. J. Am. Soc. Mass Spectrom. 10 , 770–781 (1999).

American Society of Brewing Chemists. Sensory Analysis Methods. (American Society of Brewing Chemists, St. Paul, MN, U.S.A., 1992).

McAuley, J., Leskovec, J. & Jurafsky, D. Learning Attitudes and Attributes from Multi-Aspect Reviews. Preprint at https://doi.org/10.48550/arXiv.1210.3926 (2012).

Meilgaard, M. C., Carr, B. T. & Carr, B. T. Sensory Evaluation Techniques. (CRC Press, Boca Raton). https://doi.org/10.1201/b16452 (2014).

Schreurs, M. et al. Data from: Predicting and improving complex beer flavor through machine learning. Zenodo https://doi.org/10.5281/zenodo.10653704 (2024).

Download references

Acknowledgements

We thank all lab members for their discussions and thank all tasting panel members for their contributions. Special thanks go out to Dr. Karin Voordeckers for her tremendous help in proofreading and improving the manuscript. M.S. was supported by a Baillet-Latour fellowship, L.C. acknowledges financial support from KU Leuven (C16/17/006), F.A.T. was supported by a PhD fellowship from FWO (1S08821N). Research in the lab of K.J.V. is supported by KU Leuven, FWO, VIB, VLAIO and the Brewing Science Serves Health Fund. Research in the lab of T.W. is supported by FWO (G.0A51.15) and KU Leuven (C16/17/006).

Author information

These authors contributed equally: Michiel Schreurs, Supinya Piampongsant, Miguel Roncoroni.

Authors and Affiliations

VIB—KU Leuven Center for Microbiology, Gaston Geenslaan 1, B-3001, Leuven, Belgium

Michiel Schreurs, Supinya Piampongsant, Miguel Roncoroni, Lloyd Cool, Beatriz Herrera-Malaver, Florian A. Theßeling & Kevin J. Verstrepen

CMPG Laboratory of Genetics and Genomics, KU Leuven, Gaston Geenslaan 1, B-3001, Leuven, Belgium

Leuven Institute for Beer Research (LIBR), Gaston Geenslaan 1, B-3001, Leuven, Belgium

Laboratory of Socioecology and Social Evolution, KU Leuven, Naamsestraat 59, B-3000, Leuven, Belgium

Lloyd Cool, Christophe Vanderaa & Tom Wenseleers

VIB Bioinformatics Core, VIB, Rijvisschestraat 120, B-9052, Ghent, Belgium

Łukasz Kreft & Alexander Botzki

AB InBev SA/NV, Brouwerijplein 1, B-3000, Leuven, Belgium

Philippe Malcorps & Luk Daenen

You can also search for this author in PubMed   Google Scholar

Contributions

S.P., M.S. and K.J.V. conceived the experiments. S.P., M.S. and K.J.V. designed the experiments. S.P., M.S., M.R., B.H. and F.A.T. performed the experiments. S.P., M.S., L.C., C.V., L.K., A.B., P.M., L.D., T.W. and K.J.V. contributed analysis ideas. S.P., M.S., L.C., C.V., T.W. and K.J.V. analyzed the data. All authors contributed to writing the manuscript.

Corresponding author

Correspondence to Kevin J. Verstrepen .

Ethics declarations

Competing interests.

K.J.V. is affiliated with bar.on. The other authors declare no competing interests.

Peer review

Peer review information.

Nature Communications thanks Florian Bauer, Andrew John Macintosh and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary information, peer review file, description of additional supplementary files, supplementary data 1, supplementary data 2, supplementary data 3, supplementary data 4, supplementary data 5, supplementary data 6, supplementary data 7, reporting summary, source data, source data, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Schreurs, M., Piampongsant, S., Roncoroni, M. et al. Predicting and improving complex beer flavor through machine learning. Nat Commun 15 , 2368 (2024). https://doi.org/10.1038/s41467-024-46346-0

Download citation

Received : 30 October 2023

Accepted : 21 February 2024

Published : 26 March 2024

DOI : https://doi.org/10.1038/s41467-024-46346-0

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing: Translational Research newsletter — top stories in biotechnology, drug discovery and pharma.

Why Taiwan Was So Prepared for a Powerful Earthquake

Decades of learning from disasters, tightening building codes and increasing public awareness may have helped its people better weather strong quakes.

Search-and-rescue teams recover a body from a leaning building in Hualien, Taiwan. Thanks to improvements in building codes after past earthquakes, many structures withstood Wednesday’s quake. Credit...

Supported by

• Share full article

By Chris Buckley ,  Meaghan Tobin and Siyi Zhao

Photographs by Lam Yik Fei

Chris Buckley reported from the city of Hualien, Meaghan Tobin from Taipei, in Taiwan.

• April 4, 2024

When the largest earthquake in Taiwan in half a century struck off its east coast, the buildings in the closest city, Hualien, swayed and rocked. As more than 300 aftershocks rocked the island over the next 24 hours to Thursday morning, the buildings shook again and again.

But for the most part, they stood.

Even the two buildings that suffered the most damage remained largely intact, allowing residents to climb to safety out the windows of upper stories. One of them, the rounded, red brick Uranus Building, which leaned precariously after its first floors collapsed, was mostly drawing curious onlookers.

The building is a reminder of how much Taiwan has prepared for disasters like the magnitude-7.4 earthquake that jolted the island on Wednesday. Perhaps because of improvements in building codes, greater public awareness and highly trained search-and-rescue operations — and, likely, a dose of good luck — the casualty figures were relatively low. By Thursday, 10 people had died and more than 1,000 others were injured. Several dozen were missing.

“Similar level earthquakes in other societies have killed far more people,” said Daniel Aldrich , a director of the Global Resilience Institute at Northeastern University. Of Taiwan, he added: “And most of these deaths, it seems, have come from rock slides and boulders, rather than building collapses.”

Across the island, rail traffic had resumed by Thursday, including trains to Hualien. Workers who had been stuck in a rock quarry were lifted out by helicopter. Roads were slowly being repaired. Hundreds of people were stranded at a hotel near a national park because of a blocked road, but they were visited by rescuers and medics.

On Thursday in Hualien city, the area around the Uranus Building was sealed off, while construction workers tried to prevent the leaning structure from toppling completely. First they placed three-legged concrete blocks that resembled giant Lego pieces in front of the building, and then they piled dirt and rocks on top of those blocks with excavators.

“We came to see for ourselves how serious it was, why it has tilted,” said Chang Mei-chu, 66, a retiree who rode a scooter with her husband Lai Yung-chi, 72, to the building on Thursday. Mr. Lai said he was a retired builder who used to install power and water pipes in buildings, and so he knew about building standards. The couple’s apartment, near Hualien’s train station, had not been badly damaged, he said.

“I wasn’t worried about our building, because I know they paid attention to earthquake resistance when building it. I watched them pour the cement to make sure,” Mr. Lai said. “There have been improvements. After each earthquake, they raise the standards some more.”

It was possible to walk for city blocks without seeing clear signs of the powerful earthquake. Many buildings remained intact, some of them old and weather-worn; others modern, multistory concrete-and-glass structures. Shops were open, selling coffee, ice cream and betel nuts. Next to the Uranus Building, a popular night market with food stalls offering fried seafood, dumplings and sweets was up and running by Thursday evening.

Earthquakes are unavoidable in Taiwan, which sits on multiple active faults. Decades of work learning from other disasters, implementing strict building codes and increasing public awareness have gone into helping its people weather frequent strong quakes.

Not far from the Uranus Building, for example, officials had inspected a building with cracked pillars and concluded that it was dangerous to stay in. Residents were given 15 minutes to dash inside and retrieve as many belongings as they could. Some ran out with computers, while others threw bags of clothes out of windows onto the street, which was also still littered with broken glass and cement fragments from the quake.

One of its residents, Chen Ching-ming, a preacher at a church next door, said he thought the building might be torn down. He was able to salvage a TV and some bedding, which now sat on the sidewalk, and was preparing to go back in for more. “I’ll lose a lot of valuable things — a fridge, a microwave, a washing machine,” he said. “All gone.”

Requirements for earthquake resistance have been built into Taiwan’s building codes since 1974. In the decades since, the writers of Taiwan’s building code also applied lessons learned from other major earthquakes around the world, including in Mexico and Los Angeles, to strengthen Taiwan’s code.

After more than 2,400 people were killed and at least 10,000 others injured during the Chi-Chi quake of 1999, thousands of buildings built before the quake were reviewed and reinforced. After another strong quake in 2018 in Hualien, the government ordered a new round of building inspections. Since then, multiple updates to the building code have been released.

“We have retrofitted more than 10,000 school buildings in the last 20 years,” said Chung-Che Chou, the director general of the National Center for Research on Earthquake Engineering in Taipei.

The government had also helped reinforce private apartment buildings over the past six years by adding new steel braces and increasing column and beam sizes, Dr. Chou said. Not far from the buildings that partially collapsed in Hualien, some of the older buildings that had been retrofitted in this way survived Wednesday’s quake, he said.

The result of all this is that even Taiwan’s tallest skyscrapers can withstand regular seismic jolts. The capital city’s most iconic building, Taipei 101, once the tallest building in the world, was engineered to stand through typhoon winds and frequent quakes. Still, some experts say that more needs to be done to either strengthen or demolish structures that don’t meet standards, and such calls have grown louder in the wake of the latest earthquake.

Taiwan has another major reason to protect its infrastructure: It is home to the majority of production for the Taiwan Semiconductor Manufacturing Company, the world’s largest maker of advanced computer chips. The supply chain for electronics from smartphones to cars to fighter jets rests on the output of TSMC’s factories, which make these chips in facilities that cost billions of dollars to build.

The 1999 quake also prompted TSMC to take extra steps to insulate its factories from earthquake damage. The company made major structural adjustments and adopted new technologies like early warning systems. When another large quake struck the southern city of Kaohsiung in February 2016, TSMC’s two nearby factories survived without structural damage.

Taiwan has made strides in its response to disasters, experts say. In the first 24 hours after the quake, rescuers freed hundreds of people who were trapped in cars in between rockfalls on the highway and stranded on mountain ledges in rock quarries.

“After years of hard work on capacity building, the overall performance of the island has improved significantly,” said Bruce Wong, an emergency management consultant in Hong Kong. Taiwan’s rescue teams have come to specialize in complex efforts, he said, and it has also been able to tap the skills of trained volunteers.

Taiwan’s resilience also stems from a strong civil society that is involved in public preparedness for disasters.

Ou Chi-hu, a member of a group of Taiwanese military veterans, was helping distribute water and other supplies at a school that was serving as a shelter for displaced residents in Hualien. He said that people had learned from the 1999 earthquake how to be more prepared.

“They know to shelter in a corner of the room or somewhere else safer,” he said. Many residents also keep a bag of essentials next to their beds, and own fire extinguishers, he added.

Around him, a dozen or so other charities and groups were offering residents food, money, counseling and childcare. The Tzu Chi Foundation, a large Taiwanese Buddhist charity, provided tents for families to use inside the school hall so they could have more privacy. Huang Yu-chi, a disaster relief manager with the foundation, said nonprofits had learned from earlier disasters.

“Now we’re more systematic and have a better idea of disaster prevention,” Mr. Huang said.

Mike Ives contributed reporting from Seoul.

Chris Buckley , the chief China correspondent for The Times, reports on China and Taiwan from Taipei, focused on politics, social change and security and military issues. More about Chris Buckley

Meaghan Tobin is a technology correspondent for The Times based in Taipei, covering business and tech stories in Asia with a focus on China. More about Meaghan Tobin

Siyi Zhao is a reporter and researcher who covers news in mainland China for The Times in Seoul. More about Siyi Zhao

Advertisement